Shape-constrained Symbolic Regression with NSGA-III

Shape-constrained symbolic regression (SCSR) allows to include prior knowledge into data-based modeling. This inclusion allows to ensure that certain expected behavior is better reflected by the resulting models. The expected behavior is defined via constraints, which refer to the function form e.g. monotonicity, concavity, convexity or the models image boundaries. In addition to the advantage of obtaining more robust and reliable models due to defining constraints over the functions shape, the use of SCSR allows to find models which are more robust to noise and have a better extrapolation behavior. This paper presents a mutlicriterial approach to minimize the approximation error as well as the constraint violations. Explicitly the two algorithms NSGA-II and NSGA-III are implemented and compared against each other in terms of model quality and runtime. Both algorithms are capable of dealing with multiple objectives, whereas NSGA-II is a well established multi-objective approach performing well on instances with up-to 3 objectives. NSGA-III is an extension of the NSGA-II algorithm and was developed to handle problems with "many" objectives (more than 3 objectives). Both algorithms are executed on a selected set of benchmark instances from physics textbooks. The results indicate that both algorithms are able to find largely feasible solutions and NSGA-III provides slight improvements in terms of model quality. Moreover, an improvement in runtime can be observed using the many-objective approach.

Using Shape Constraints for Improving Symbolic Regression Models

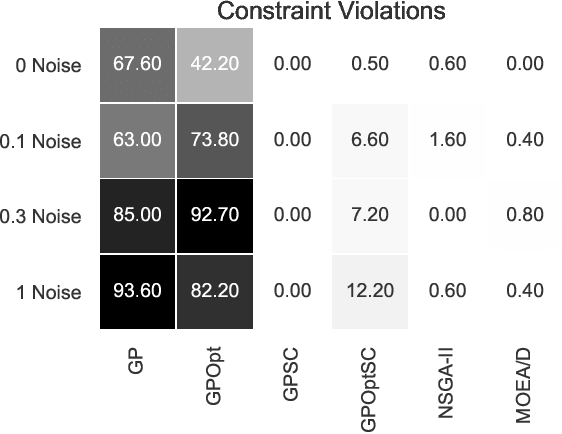
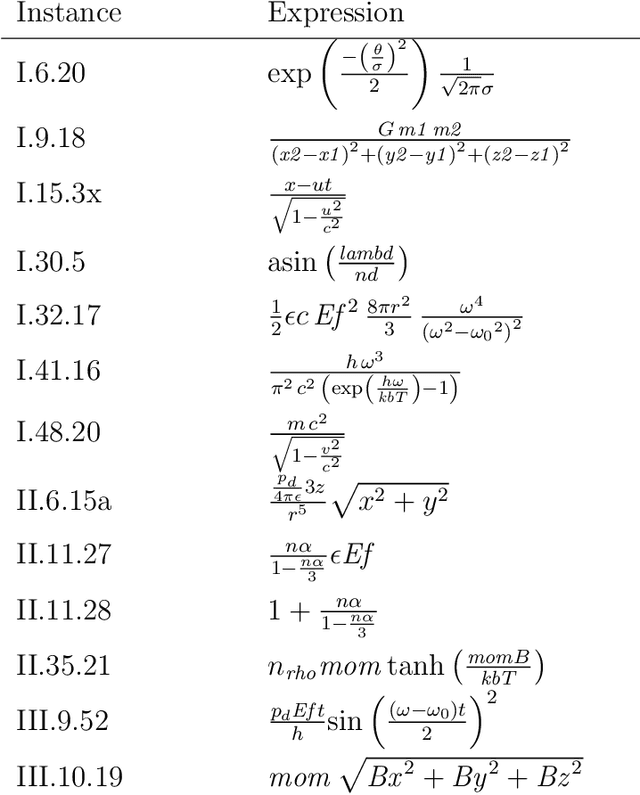
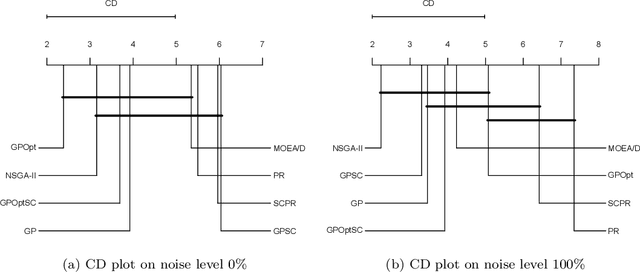
We describe and analyze algorithms for shape-constrained symbolic regression, which allows the inclusion of prior knowledge about the shape of the regression function. This is relevant in many areas of engineering -- in particular whenever a data-driven model obtained from measurements must have certain properties (e.g. positivity, monotonicity or convexity/concavity). We implement shape constraints using a soft-penalty approach which uses multi-objective algorithms to minimize constraint violations and training error. We use the non-dominated sorting genetic algorithm (NSGA-II) as well as the multi-objective evolutionary algorithm based on decomposition (MOEA/D). We use a set of models from physics textbooks to test the algorithms and compare against earlier results with single-objective algorithms. The results show that all algorithms are able to find models which conform to all shape constraints. Using shape constraints helps to improve extrapolation behavior of the models.

Shape-constrained Symbolic Regression -- Improving Extrapolation with Prior Knowledge

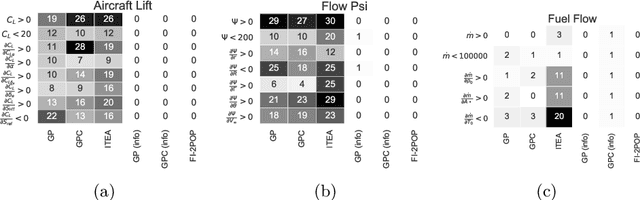
We investigate the addition of constraints on the function image and its derivatives for the incorporation of prior knowledge in symbolic regression. The approach is called shape-constrained symbolic regression and allows us to enforce e.g. monotonicity of the function over selected inputs. The aim is to find models which conform to expected behaviour and which have improved extrapolation capabilities. We demonstrate the feasibility of the idea and propose and compare two evolutionary algorithms for shape-constrained symbolic regression: i) an extension of tree-based genetic programming which discards infeasible solutions in the selection step, and ii) a two population evolutionary algorithm that separates the feasible from the infeasible solutions. In both algorithms we use interval arithmetic to approximate bounds for models and their partial derivatives. The algorithms are tested on a set of 19 synthetic and four real-world regression problems. Both algorithms are able to identify models which conform to shape constraints which is not the case for the unmodified symbolic regression algorithms. However, the predictive accuracy of models with constraints is worse on the training set and the test set. Shape-constrained polynomial regression produces the best results for the test set but also significantly larger models.