Using Shape Constraints for Improving Symbolic Regression Models
Paper and Code
Jul 20, 2021
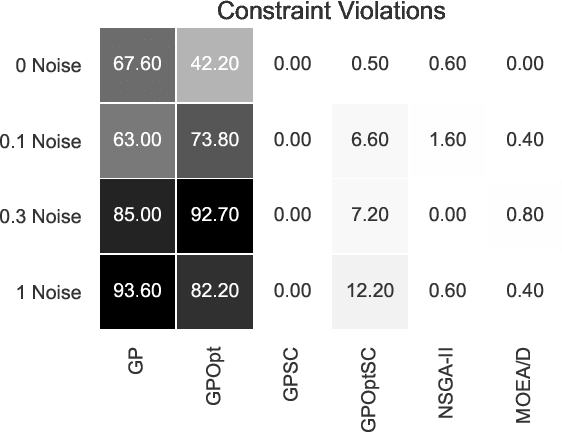
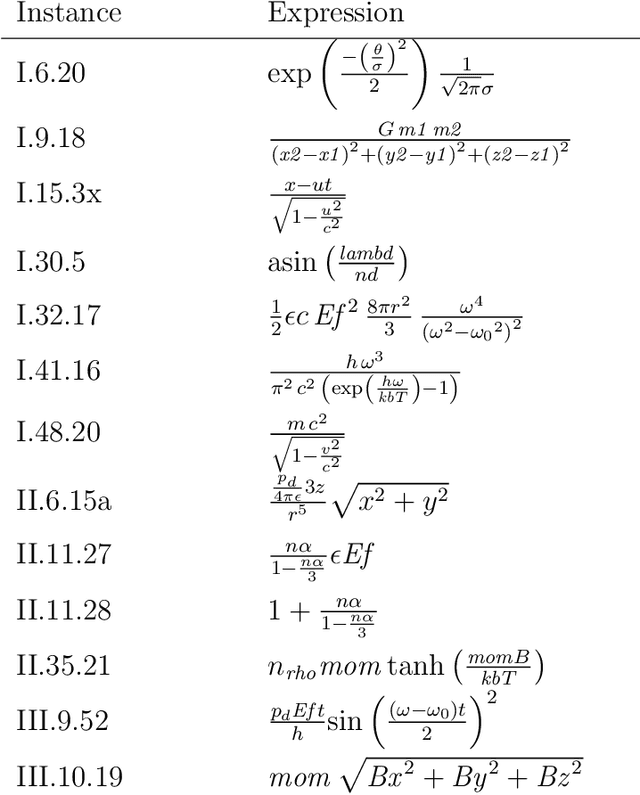
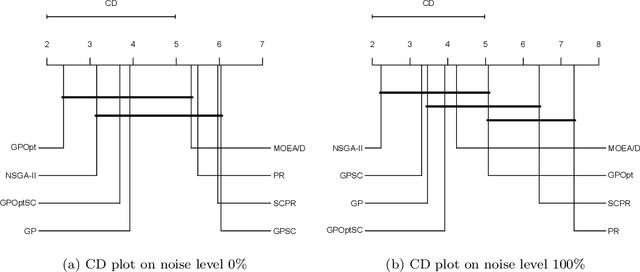
We describe and analyze algorithms for shape-constrained symbolic regression, which allows the inclusion of prior knowledge about the shape of the regression function. This is relevant in many areas of engineering -- in particular whenever a data-driven model obtained from measurements must have certain properties (e.g. positivity, monotonicity or convexity/concavity). We implement shape constraints using a soft-penalty approach which uses multi-objective algorithms to minimize constraint violations and training error. We use the non-dominated sorting genetic algorithm (NSGA-II) as well as the multi-objective evolutionary algorithm based on decomposition (MOEA/D). We use a set of models from physics textbooks to test the algorithms and compare against earlier results with single-objective algorithms. The results show that all algorithms are able to find models which conform to all shape constraints. Using shape constraints helps to improve extrapolation behavior of the models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge