Shape-constrained Symbolic Regression -- Improving Extrapolation with Prior Knowledge
Paper and Code
Mar 29, 2021
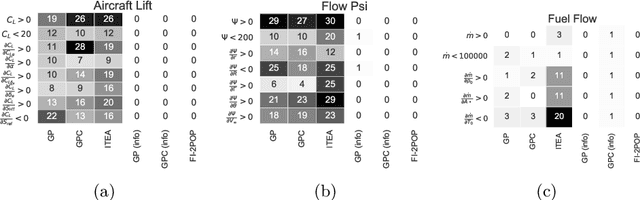
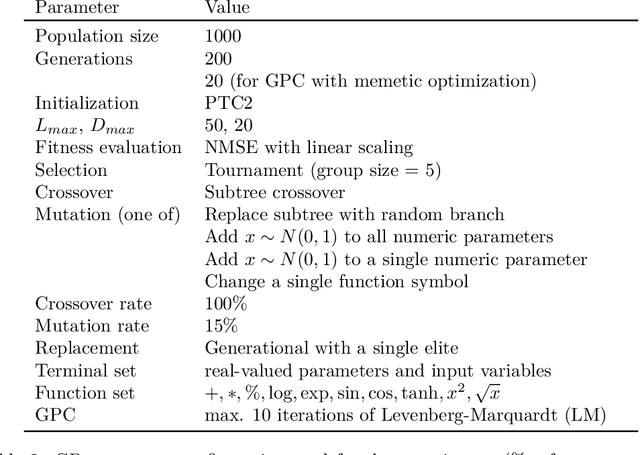
We investigate the addition of constraints on the function image and its derivatives for the incorporation of prior knowledge in symbolic regression. The approach is called shape-constrained symbolic regression and allows us to enforce e.g. monotonicity of the function over selected inputs. The aim is to find models which conform to expected behaviour and which have improved extrapolation capabilities. We demonstrate the feasibility of the idea and propose and compare two evolutionary algorithms for shape-constrained symbolic regression: i) an extension of tree-based genetic programming which discards infeasible solutions in the selection step, and ii) a two population evolutionary algorithm that separates the feasible from the infeasible solutions. In both algorithms we use interval arithmetic to approximate bounds for models and their partial derivatives. The algorithms are tested on a set of 19 synthetic and four real-world regression problems. Both algorithms are able to identify models which conform to shape constraints which is not the case for the unmodified symbolic regression algorithms. However, the predictive accuracy of models with constraints is worse on the training set and the test set. Shape-constrained polynomial regression produces the best results for the test set but also significantly larger models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge