Generalized Wick Decompositions

We review the cumulant decomposition (a way of decomposing the expectation of a product of random variables (e.g. $\mathbb{E}[XYZ]$) into a sum of terms corresponding to partitions of these variables.) and the Wick decomposition (a way of decomposing a product of (not necessarily random) variables into a sum of terms corresponding to subsets of the variables). Then we generalize each one to a new decomposition where the product function is generalized to an arbitrary function.

Localizing Model Behavior with Path Patching

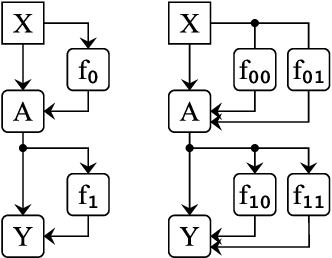
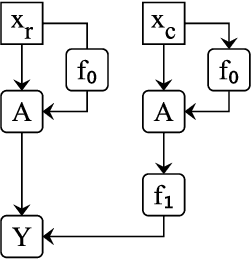
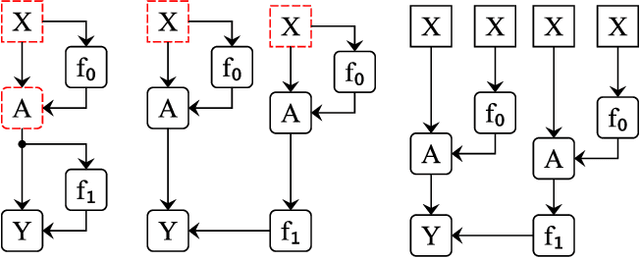
Localizing behaviors of neural networks to a subset of the network's components or a subset of interactions between components is a natural first step towards analyzing network mechanisms and possible failure modes. Existing work is often qualitative and ad-hoc, and there is no consensus on the appropriate way to evaluate localization claims. We introduce path patching, a technique for expressing and quantitatively testing a natural class of hypotheses expressing that behaviors are localized to a set of paths. We refine an explanation of induction heads, characterize a behavior of GPT-2, and open source a framework for efficiently running similar experiments.