Chris Chu
Randomized Bregman Coordinate Descent Methods for Non-Lipschitz Optimization
Jan 15, 2020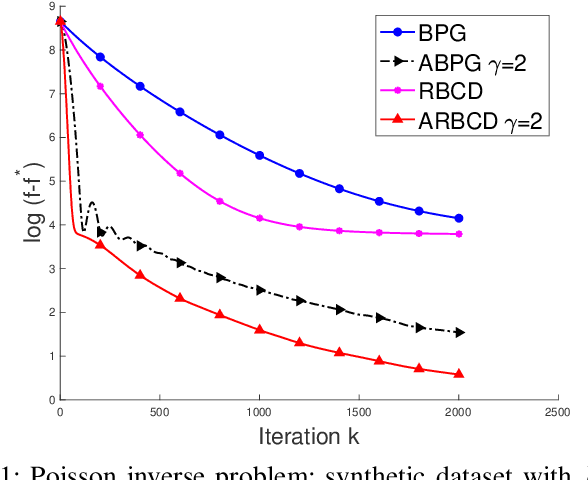
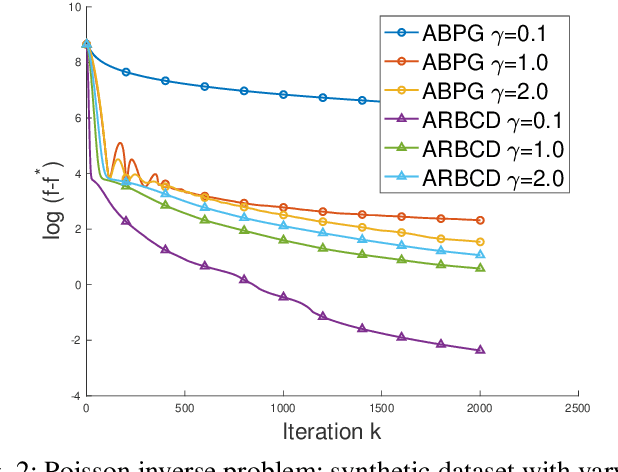
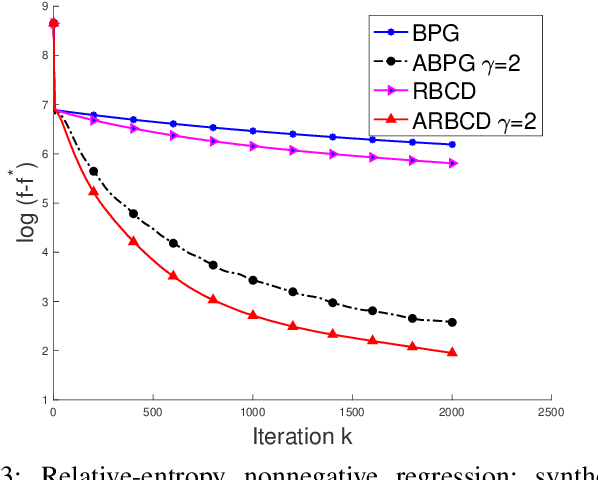
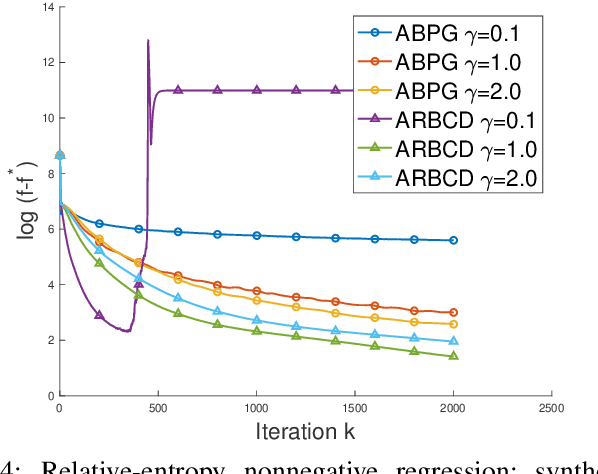
Abstract:We propose a new \textit{randomized Bregman (block) coordinate descent} (RBCD) method for minimizing a composite problem, where the objective function could be either convex or nonconvex, and the smooth part are freed from the global Lipschitz-continuous (partial) gradient assumption. Under the notion of relative smoothness based on the Bregman distance, we prove that every limit point of the generated sequence is a stationary point. Further, we show that the iteration complexity of the proposed method is $O(n\varepsilon^{-2})$ to achieve $\epsilon$-stationary point, where $n$ is the number of blocks of coordinates. If the objective is assumed to be convex, the iteration complexity is improved to $O(n\epsilon^{-1} )$. If, in addition, the objective is strongly convex (relative to the reference function), the global linear convergence rate is recovered. We also present the accelerated version of the RBCD method, which attains an $O(n\varepsilon^{-1/\gamma} )$ iteration complexity for the convex case, where the scalar $\gamma\in [1,2]$ is determined by the \textit{generalized translation variant} of the Bregman distance. Convergence analysis without assuming the global Lipschitz-continuous (partial) gradient sets our results apart from the existing works in the composite problems.
Leveraging Two Reference Functions in Block Bregman Proximal Gradient Descent for Non-convex and Non-Lipschitz Problems
Dec 16, 2019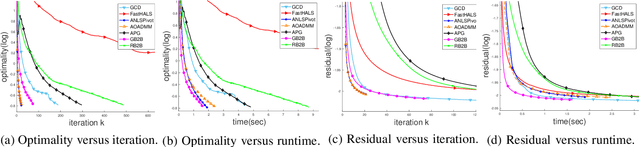
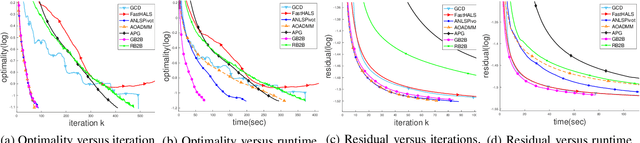
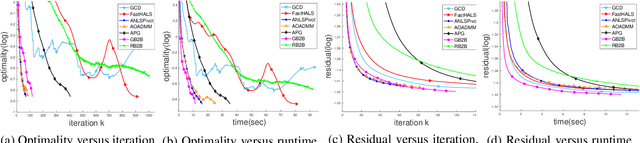
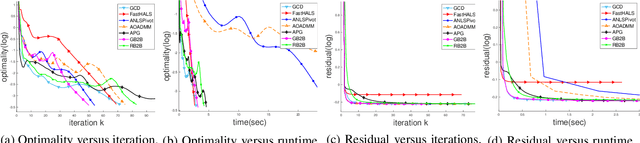
Abstract:In the applications of signal processing and data analytics, there is a wide class of non-convex problems whose objective function is freed from the common global Lipschitz continuous gradient assumption (e.g., the nonnegative matrix factorization (NMF) problem). Recently, this type of problem with some certain special structures has been solved by Bregman proximal gradient (BPG). This inspires us to propose a new Block-wise two-references Bregman proximal gradient (B2B) method, which adopts two reference functions so that a closed-form solution in the Bregman projection is obtained. Based on the relative smoothness, we prove the global convergence of the proposed algorithms for various block selection rules. In particular, we establish the global convergence rate of $O(\frac{\sqrt{s}}{\sqrt{k}})$ for the greedy and randomized block updating rule for B2B, which is $O(\sqrt{s})$ times faster than the cyclic variant, i.e., $O(\frac{s}{\sqrt{k}} )$, where $s$ is the number of blocks, and $k$ is the number of iterations. Multiple numerical results are provided to illustrate the superiority of the proposed B2B compared to the state-of-the-art works in solving NMF problems.
DID: Distributed Incremental Block Coordinate Descent for Nonnegative Matrix Factorization
Feb 25, 2018
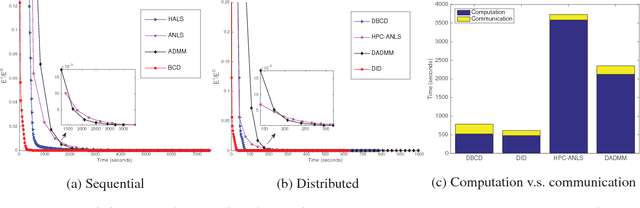

Abstract:Nonnegative matrix factorization (NMF) has attracted much attention in the last decade as a dimension reduction method in many applications. Due to the explosion in the size of data, naturally the samples are collected and stored distributively in local computational nodes. Thus, there is a growing need to develop algorithms in a distributed memory architecture. We propose a novel distributed algorithm, called \textit{distributed incremental block coordinate descent} (DID), to solve the problem. By adapting the block coordinate descent framework, closed-form update rules are obtained in DID. Moreover, DID performs updates incrementally based on the most recently updated residual matrix. As a result, only one communication step per iteration is required. The correctness, efficiency, and scalability of the proposed algorithm are verified in a series of numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge