Randomized Bregman Coordinate Descent Methods for Non-Lipschitz Optimization
Paper and Code
Jan 15, 2020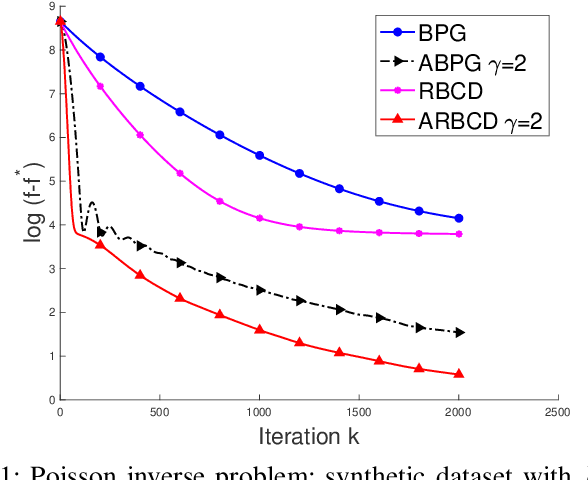
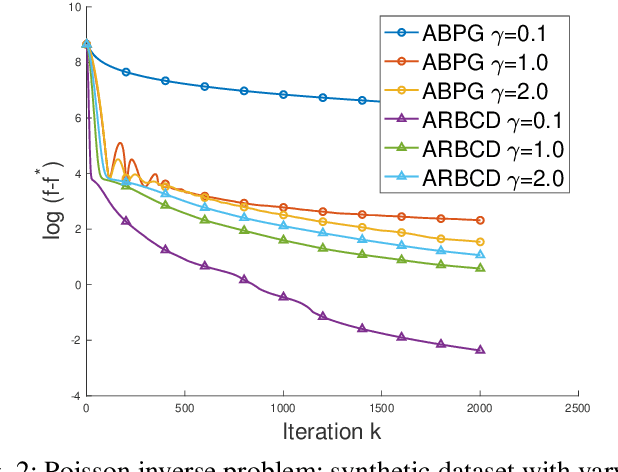
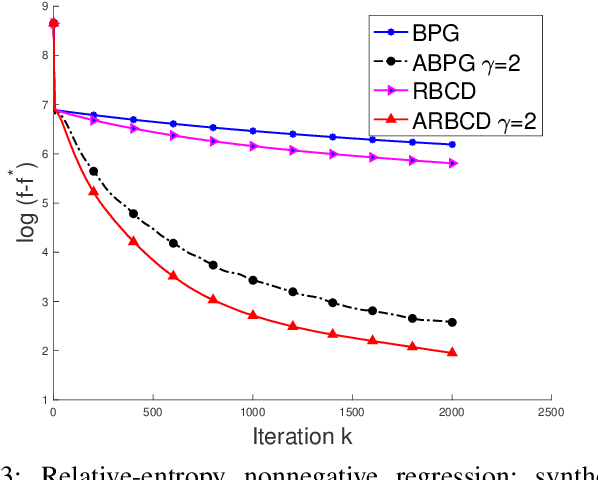
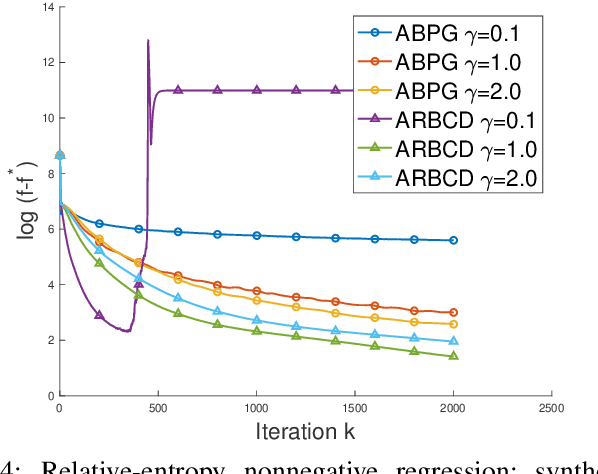
We propose a new \textit{randomized Bregman (block) coordinate descent} (RBCD) method for minimizing a composite problem, where the objective function could be either convex or nonconvex, and the smooth part are freed from the global Lipschitz-continuous (partial) gradient assumption. Under the notion of relative smoothness based on the Bregman distance, we prove that every limit point of the generated sequence is a stationary point. Further, we show that the iteration complexity of the proposed method is $O(n\varepsilon^{-2})$ to achieve $\epsilon$-stationary point, where $n$ is the number of blocks of coordinates. If the objective is assumed to be convex, the iteration complexity is improved to $O(n\epsilon^{-1} )$. If, in addition, the objective is strongly convex (relative to the reference function), the global linear convergence rate is recovered. We also present the accelerated version of the RBCD method, which attains an $O(n\varepsilon^{-1/\gamma} )$ iteration complexity for the convex case, where the scalar $\gamma\in [1,2]$ is determined by the \textit{generalized translation variant} of the Bregman distance. Convergence analysis without assuming the global Lipschitz-continuous (partial) gradient sets our results apart from the existing works in the composite problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge