REMuS-GNN: A Rotation-Equivariant Model for Simulating Continuum Dynamics

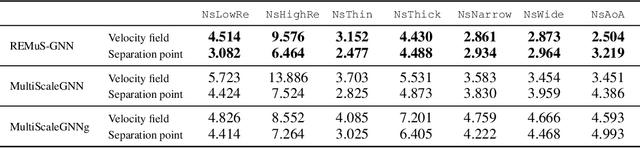
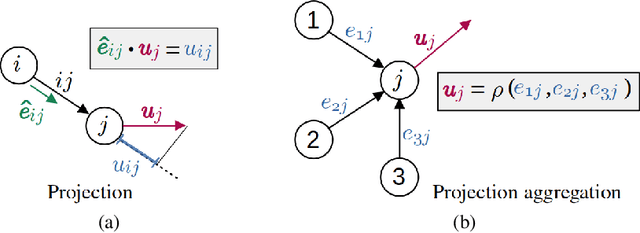
Numerical simulation is an essential tool in many areas of science and engineering, but its performance often limits application in practice or when used to explore large parameter spaces. On the other hand, surrogate deep learning models, while accelerating simulations, often exhibit poor accuracy and ability to generalise. In order to improve these two factors, we introduce REMuS-GNN, a rotation-equivariant multi-scale model for simulating continuum dynamical systems encompassing a range of length scales. REMuS-GNN is designed to predict an output vector field from an input vector field on a physical domain discretised into an unstructured set of nodes. Equivariance to rotations of the domain is a desirable inductive bias that allows the network to learn the underlying physics more efficiently, leading to improved accuracy and generalisation compared with similar architectures that lack such symmetry. We demonstrate and evaluate this method on the incompressible flow around elliptical cylinders.

Towards Fast Simulation of Environmental Fluid Mechanics with Multi-Scale Graph Neural Networks

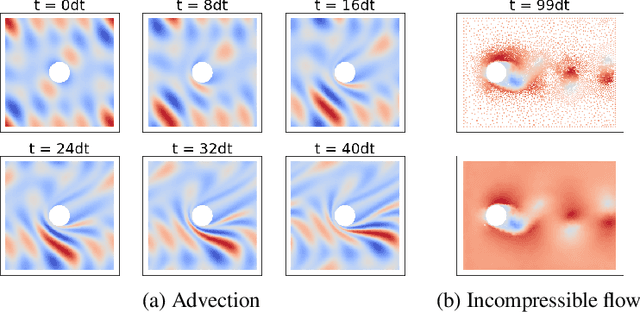
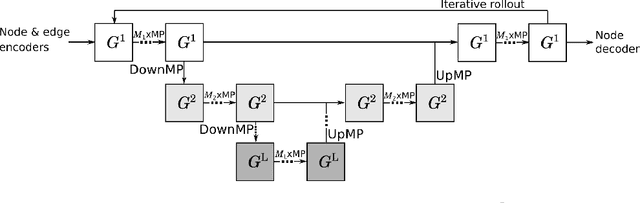
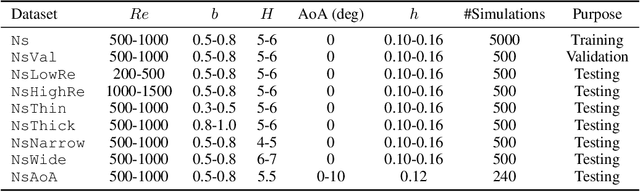
Numerical simulators are essential tools in the study of natural fluid-systems, but their performance often limits application in practice. Recent machine-learning approaches have demonstrated their ability to accelerate spatio-temporal predictions, although, with only moderate accuracy in comparison. Here we introduce MultiScaleGNN, a novel multi-scale graph neural network model for learning to infer unsteady continuum mechanics in problems encompassing a range of length scales and complex boundary geometries. We demonstrate this method on advection problems and incompressible fluid dynamics, both fundamental phenomena in oceanic and atmospheric processes. Our results show good extrapolation to new domain geometries and parameters for long-term temporal simulations. Simulations obtained with MultiScaleGNN are between two and four orders of magnitude faster than those on which it was trained.

Disentangling ODE parameters from dynamics in VAEs

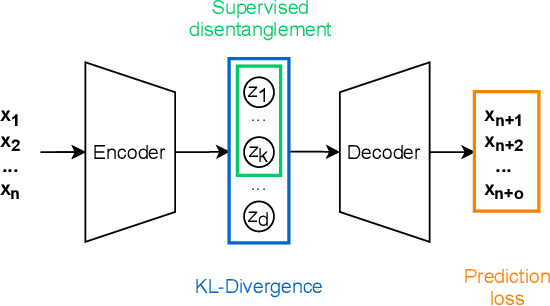
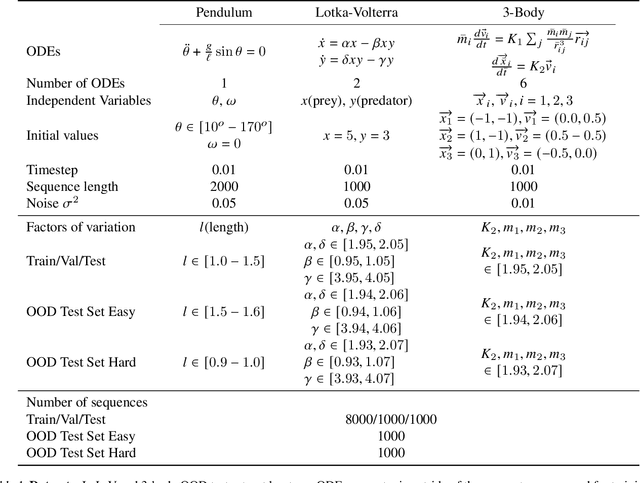
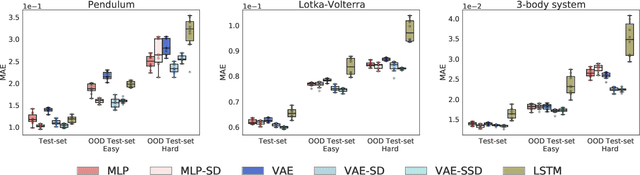
Deep networks have become increasingly of interest in dynamical system prediction, but generalization remains elusive. In this work, we consider the physical parameters of ODEs as factors of variation of the data generating process. By leveraging ideas from supervised disentanglement in VAEs, we aim to separate the ODE parameters from the dynamics in the latent space. Experiments show that supervised disentanglement allows VAEs to capture the variability in the dynamics and extrapolate better to ODE parameter spaces that were not present in the training data.

Simulating Continuum Mechanics with Multi-Scale Graph Neural Networks

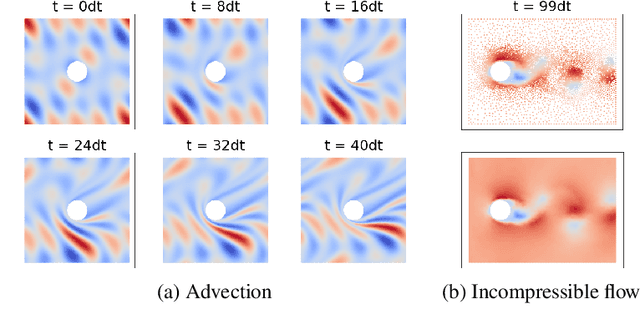
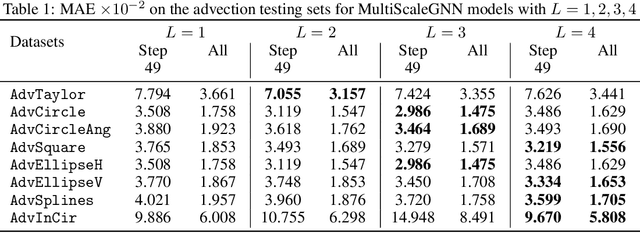
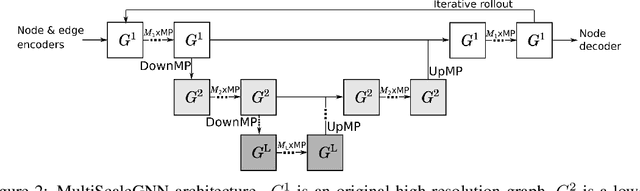
Continuum mechanics simulators, numerically solving one or more partial differential equations, are essential tools in many areas of science and engineering, but their performance often limits application in practice. Recent modern machine learning approaches have demonstrated their ability to accelerate spatio-temporal predictions, although, with only moderate accuracy in comparison. Here we introduce MultiScaleGNN, a novel multi-scale graph neural network model for learning to infer unsteady continuum mechanics. MultiScaleGNN represents the physical domain as an unstructured set of nodes, and it constructs one or more graphs, each of them encoding different scales of spatial resolution. Successive learnt message passing between these graphs improves the ability of GNNs to capture and forecast the system state in problems encompassing a range of length scales. Using graph representations, MultiScaleGNN can impose periodic boundary conditions as an inductive bias on the edges in the graphs, and achieve independence to the nodes' positions. We demonstrate this method on advection problems and incompressible fluid dynamics. Our results show that the proposed model can generalise from uniform advection fields to high-gradient fields on complex domains at test time and infer long-term Navier-Stokes solutions within a range of Reynolds numbers. Simulations obtained with MultiScaleGNN are between two and four orders of magnitude faster than the ones on which it was trained.

Simulating Surface Wave Dynamics with Convolutional Networks

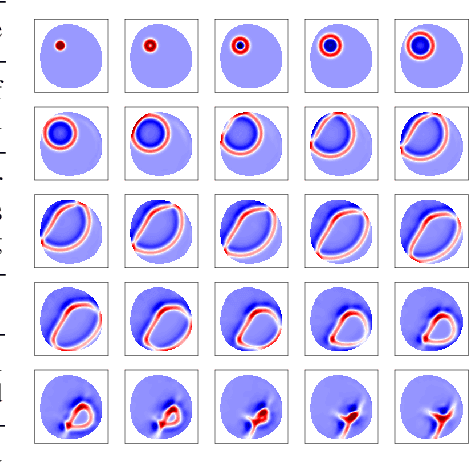
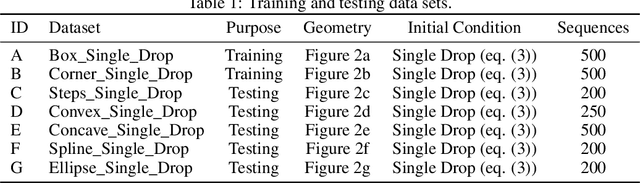
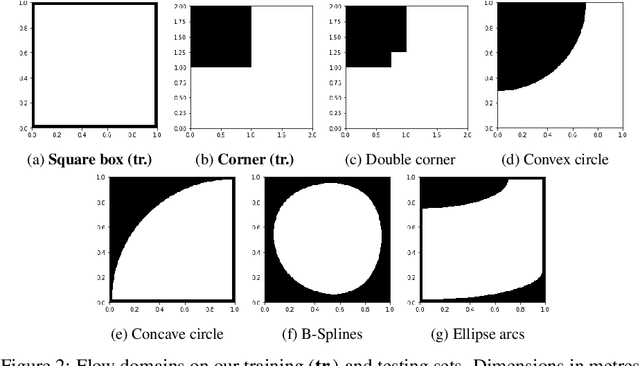
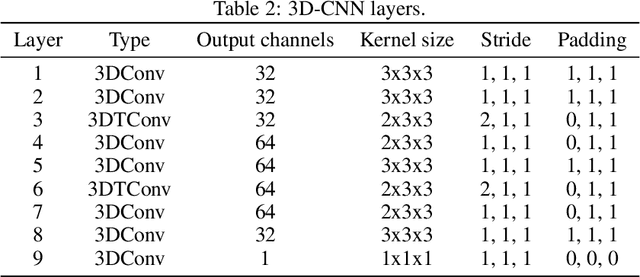
We investigate the performance of fully convolutional networks to simulate the motion and interaction of surface waves in open and closed complex geometries. We focus on a U-Net architecture and analyse how well it generalises to geometric configurations not seen during training. We demonstrate that a modified U-Net architecture is capable of accurately predicting the height distribution of waves on a liquid surface within curved and multi-faceted open and closed geometries, when only simple box and right-angled corner geometries were seen during training. We also consider a separate and independent 3D CNN for performing time-interpolation on the predictions produced by our U-Net. This allows generating simulations with a smaller time-step size than the one the U-Net has been trained for.

Comparing recurrent and convolutional neural networks for predicting wave propagation

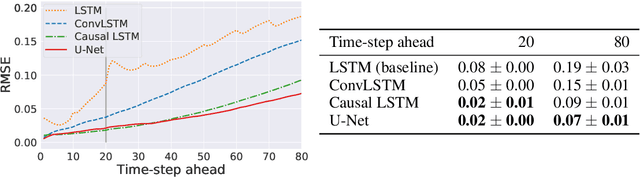
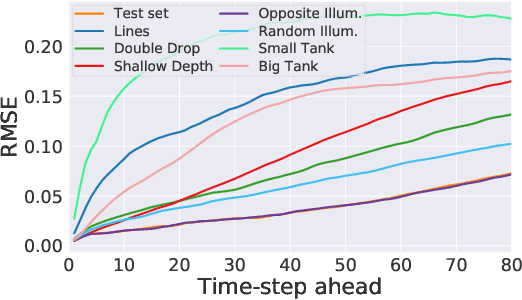
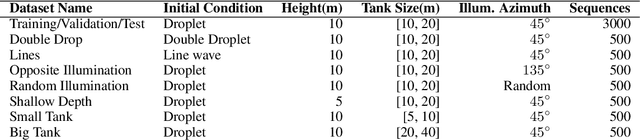
Dynamical systems can be modelled by partial differential equations and numerical computations are used everywhere in science and engineering. In this work, we investigate the performance of recurrent and convolutional deep neural network architectures to predict the surface waves. The system is governed by the Saint-Venant equations. We improve on the long-term prediction over previous methods while keeping the inference time at a fraction of numerical simulations. We also show that convolutional networks perform at least as well as recurrent networks in this task. Finally, we assess the generalisation capability of each network by extrapolating in longer time-frames and in different physical settings.