Edge of chaos as a guiding principle for modern neural network training

The success of deep neural networks in real-world problems has prompted many attempts to explain their training dynamics and generalization performance, but more guiding principles for the training of neural networks are still needed. Motivated by the edge of chaos principle behind the optimal performance of neural networks, we study the role of various hyperparameters in modern neural network training algorithms in terms of the order-chaos phase diagram. In particular, we study a fully analytical feedforward neural network trained on the widely adopted Fashion-MNIST dataset, and study the dynamics associated with the hyperparameters in back-propagation during the training process. We find that for the basic algorithm of stochastic gradient descent with momentum, in the range around the commonly used hyperparameter values, clear scaling relations are present with respect to the training time during the ordered phase in the phase diagram, and the model's optimal generalization power at the edge of chaos is similar across different training parameter combinations. In the chaotic phase, the same scaling no longer exists. The scaling allows us to choose the training parameters to achieve faster training without sacrificing performance. In addition, we find that the commonly used model regularization method - weight decay - effectively pushes the model towards the ordered phase to achieve better performance. Leveraging on this fact and the scaling relations in the other hyperparameters, we derived a principled guideline for hyperparameter determination, such that the model can achieve optimal performance by saturating it at the edge of chaos. Demonstrated on this simple neural network model and training algorithm, our work improves the understanding of neural network training dynamics, and can potentially be extended to guiding principles of more complex model architectures and algorithms.

Optimal Machine Intelligence Near the Edge of Chaos

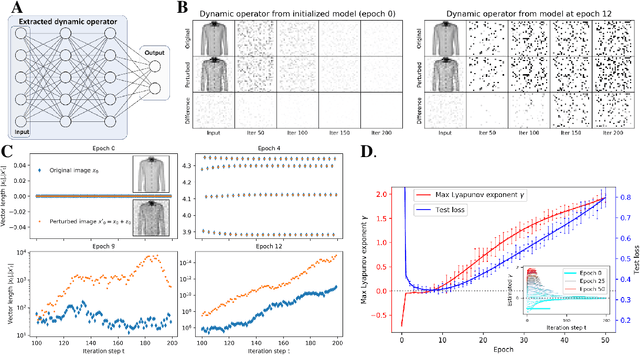
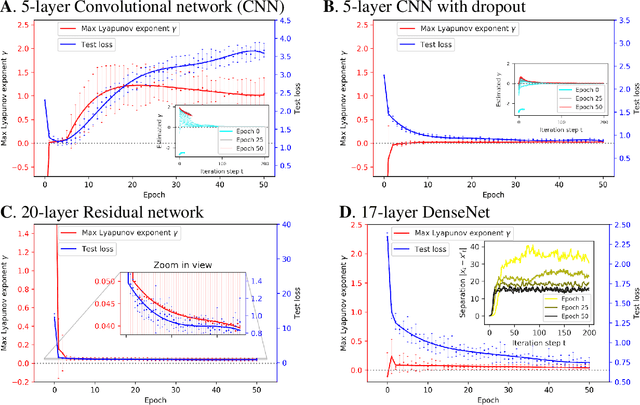
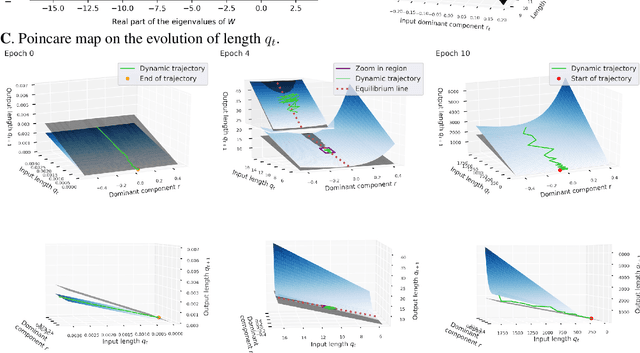
It has long been suggested that living systems, in particular the brain, may operate near some critical point. How about machines? Through dynamical stability analysis on various computer vision models, we find direct evidence that optimal deep neural network performance occur near the transition point separating stable and chaotic attractors. In fact modern neural network architectures push the model closer to this edge of chaos during the training process. Our dissection into their fully connected layers reveals that they achieve the stability transition through self-adjusting an oscillation-diffusion process embedded in the weights. Further analogy to the logistic map leads us to believe that the optimality near the edge of chaos is a consequence of maximal diversity of stable states, which maximize the effective expressivity.