Optimal Machine Intelligence Near the Edge of Chaos

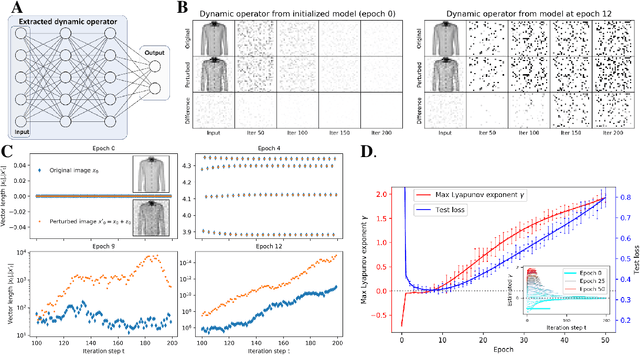
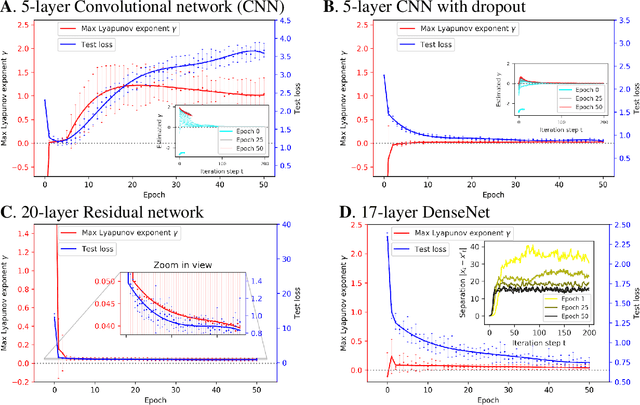
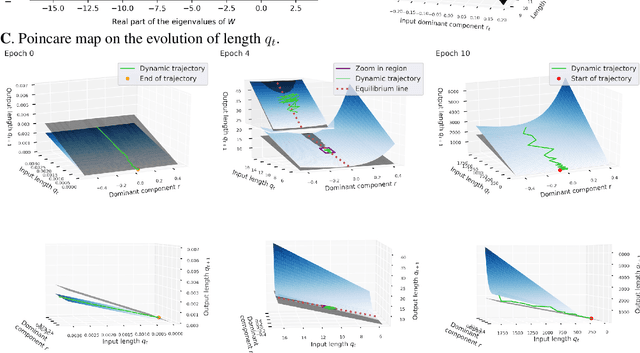
It has long been suggested that living systems, in particular the brain, may operate near some critical point. How about machines? Through dynamical stability analysis on various computer vision models, we find direct evidence that optimal deep neural network performance occur near the transition point separating stable and chaotic attractors. In fact modern neural network architectures push the model closer to this edge of chaos during the training process. Our dissection into their fully connected layers reveals that they achieve the stability transition through self-adjusting an oscillation-diffusion process embedded in the weights. Further analogy to the logistic map leads us to believe that the optimality near the edge of chaos is a consequence of maximal diversity of stable states, which maximize the effective expressivity.