A semidefinite programming approach for robust elliptic localization

This short communication addresses the problem of elliptic localization with outlier measurements, whose occurrences are prevalent in various location-enabled applications and can significantly compromise the positioning performance if not adequately handled. In contrast to the reliance on $M$-estimation adopted in the majority of existing solutions, we take a different path, specifically exploring the worst-case robust approximation criterion, to bolster resistance of the elliptic location estimator against outliers. From a geometric standpoint, our method boils down to pinpointing the Chebyshev center of the feasible set determined by the available bistatic ranges with bounded measurement errors. For a practical approach to the associated min-max problem, we convert it into the well-established convex optimization framework of semidefinite programming (SDP). Numerical simulations confirm that our SDP-based technique can outperform a number of existing elliptic localization schemes in terms of positioning accuracy in Gaussian mixture noise, a common type of impulsive interference in the context of range-based localization.

l0-norm Based Centers Selection for Training Fault Tolerant RBF Networks and Selecting Centers

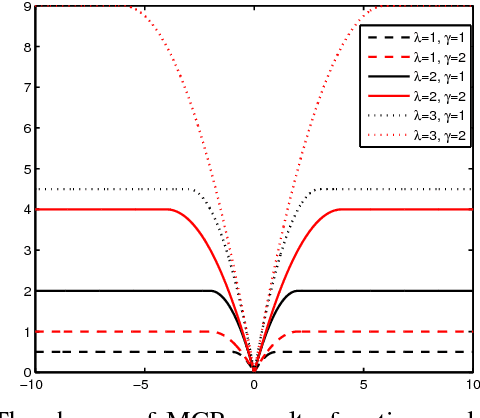
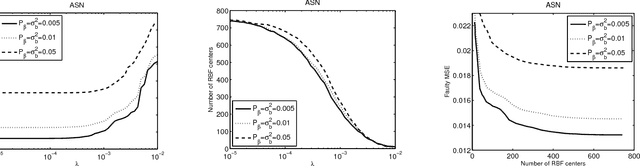
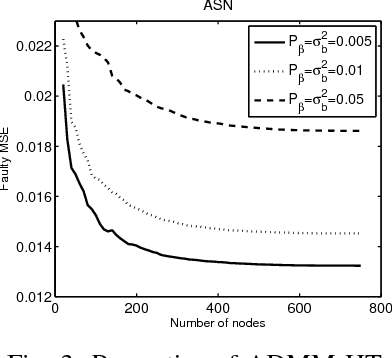
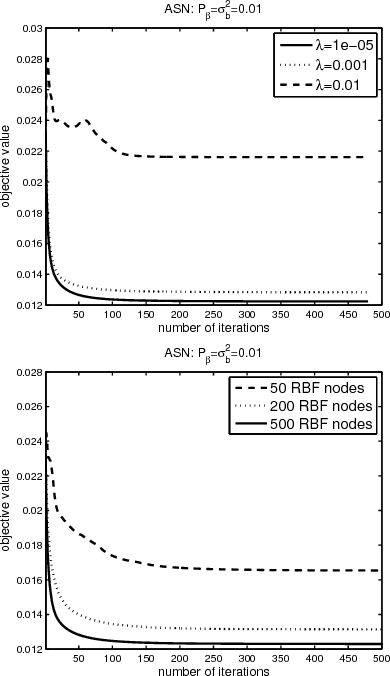
The aim of this paper is to train an RBF neural network and select centers under concurrent faults. It is well known that fault tolerance is a very attractive property for neural networks. And center selection is an important procedure during the training process of an RBF neural network. In this paper, we devise two novel algorithms to address these two issues simultaneously. Both of them are based on the ADMM framework. In the first method, the minimax concave penalty (MCP) function is introduced to select centers. In the second method, an l0-norm term is directly used, and the hard threshold (HT) is utilized to address the l0-norm term. Under several mild conditions, we can prove that both methods can globally converge to a unique limit point. Simulation results show that, under concurrent fault, the proposed algorithms are superior to many existing methods.

Fast L1-Minimization Algorithm for Sparse Approximation Based on an Improved LPNN-LCA framework

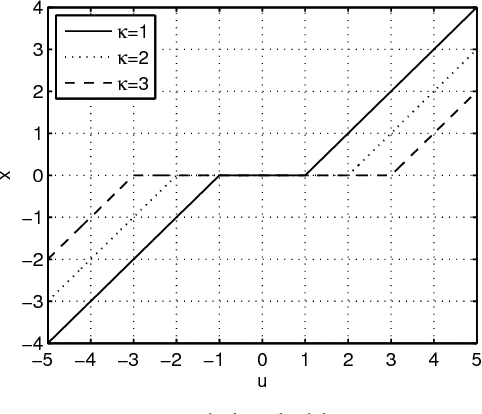
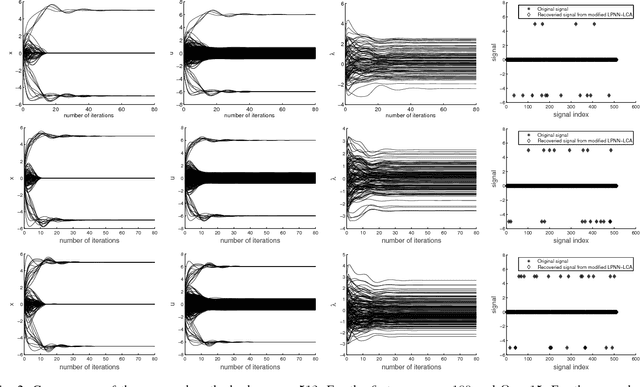
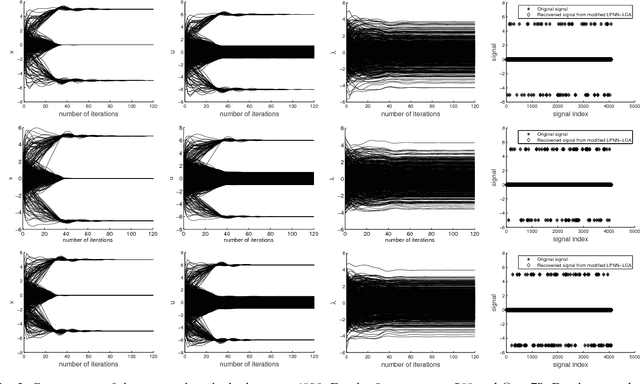
The aim of sparse approximation is to estimate a sparse signal according to the measurement matrix and an observation vector. It is widely used in data analytics, image processing, and communication, etc. Up to now, a lot of research has been done in this area, and many off-the-shelf algorithms have been proposed. However, most of them cannot offer a real-time solution. To some extent, this shortcoming limits its application prospects. To address this issue, we devise a novel sparse approximation algorithm based on Lagrange programming neural network (LPNN), locally competitive algorithm (LCA), and projection theorem. LPNN and LCA are both analog neural network which can help us get a real-time solution. The non-differentiable objective function can be solved by the concept of LCA. Utilizing the projection theorem, we further modify the dynamics and proposed a new system with global asymptotic stability. Simulation results show that the proposed sparse approximation method has the real-time solutions with satisfactory MSEs.