Fast L1-Minimization Algorithm for Sparse Approximation Based on an Improved LPNN-LCA framework
Paper and Code
May 30, 2018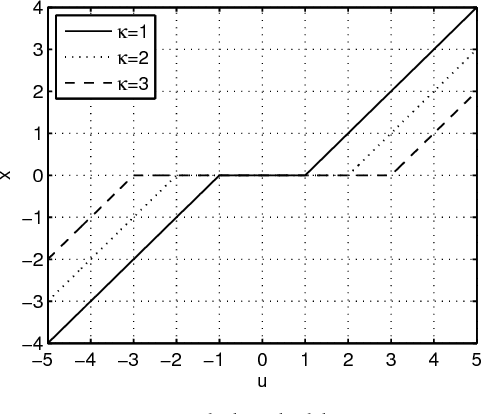
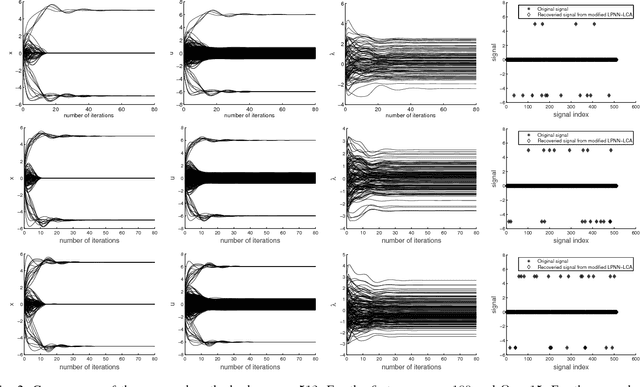
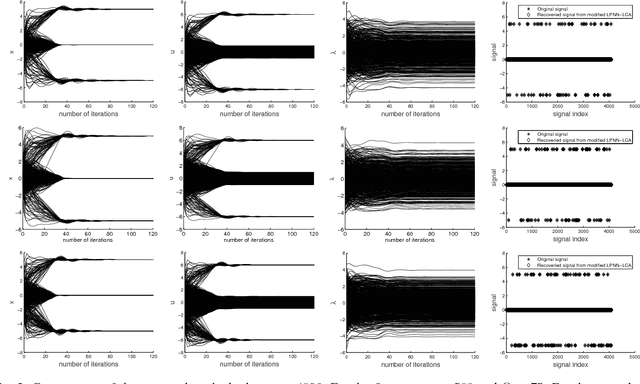

The aim of sparse approximation is to estimate a sparse signal according to the measurement matrix and an observation vector. It is widely used in data analytics, image processing, and communication, etc. Up to now, a lot of research has been done in this area, and many off-the-shelf algorithms have been proposed. However, most of them cannot offer a real-time solution. To some extent, this shortcoming limits its application prospects. To address this issue, we devise a novel sparse approximation algorithm based on Lagrange programming neural network (LPNN), locally competitive algorithm (LCA), and projection theorem. LPNN and LCA are both analog neural network which can help us get a real-time solution. The non-differentiable objective function can be solved by the concept of LCA. Utilizing the projection theorem, we further modify the dynamics and proposed a new system with global asymptotic stability. Simulation results show that the proposed sparse approximation method has the real-time solutions with satisfactory MSEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge