A semidefinite programming approach for robust elliptic localization

This short communication addresses the problem of elliptic localization with outlier measurements, whose occurrences are prevalent in various location-enabled applications and can significantly compromise the positioning performance if not adequately handled. In contrast to the reliance on $M$-estimation adopted in the majority of existing solutions, we take a different path, specifically exploring the worst-case robust approximation criterion, to bolster resistance of the elliptic location estimator against outliers. From a geometric standpoint, our method boils down to pinpointing the Chebyshev center of the feasible set determined by the available bistatic ranges with bounded measurement errors. For a practical approach to the associated min-max problem, we convert it into the well-established convex optimization framework of semidefinite programming (SDP). Numerical simulations confirm that our SDP-based technique can outperform a number of existing elliptic localization schemes in terms of positioning accuracy in Gaussian mixture noise, a common type of impulsive interference in the context of range-based localization.

Robust Time-of-Arrival Localization via ADMM

This article considers the problem of source localization (SL) using possibly unreliable time-of-arrival (TOA) based range measurements. Adopting the strategy of statistical robustification, we formulate the TOA SL as minimization of a versatile loss that possesses resistance against the occurrence of outliers. We then present an alternating direction method of multipliers (ADMM) to tackle the nonconvex optimization problem in a computationally attractive iterative manner. Moreover, we prove that the solution obtained by the proposed ADMM will correspond to a Karush-Kuhn-Tucker point of the formulation when the algorithm converges, and discuss reasonable assumptions about the robust loss function under which the approach can be theoretically guaranteed to be convergent. Numerical investigations demonstrate the superiority of our method over many existing TOA SL schemes in terms of positioning accuracy and computational simplicity. In comparison with its competitors, the proposed ADMM is in particular observed to produce location estimates with mean squared error performance closer to the Cram\'{e}r-Rao lower bound in our simulations of impulsive noise environments.

Globally Optimized TDOA High Frequency Source Localization Based on Quasi-Parabolic Ionosphere Modeling and Collaborative Gradient Projection

We investigate the problem of high frequency (HF) source localization using the time-difference-of-arrival (TDOA) observations of ionosphere-refracted radio rays based on quasi-parabolic (QP) modeling. An unresolved but pertinent issue in such a field is that the existing gradient-type scheme can easily get trapped in local optima for practical use. This will lead to the difficulty in initializing the algorithm and finally degraded positioning performance if the starting point is inappropriately selected. In this paper, we develop a collaborative gradient projection (GP) algorithm in order to globally solve the highly nonconvex QP-based TDOA HF localization problem. The metaheuristic of particle swarm optimization (PSO) is exploited for information sharing among multiple GP models, each of which is guaranteed to work out a critical point solution to the simplified maximum likelihood formulation. Random mutations are incorporated to avoid the early convergence of PSO. Rather than treating the geolocation of HF transmitter as a pure optimization problem, we further provide workarounds for addressing the possible impairments and challenges when the proposed technique is applied in practice. Numerical results demonstrate the effectiveness of our PSO-assisted re-initialization strategy in achieving the global optimality, and the superiority of our method over its competitor in terms of positioning accuracy.

Two Efficient and Easy-to-Use NLOS Mitigation Solutions to Indoor 3-D AOA-Based Localization

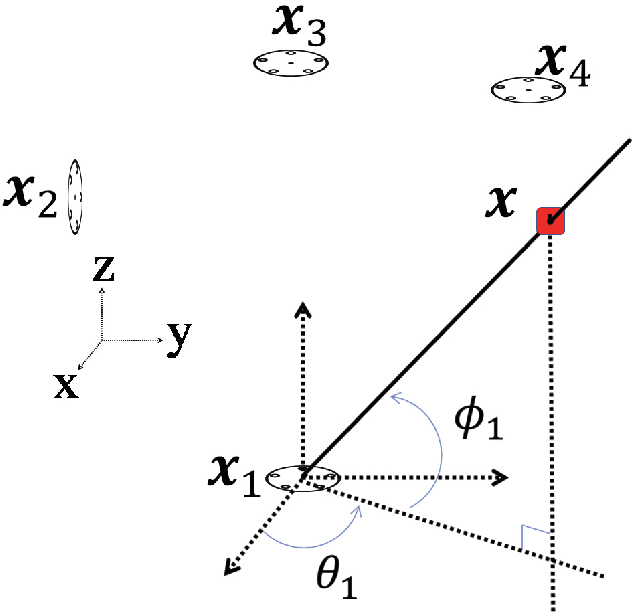
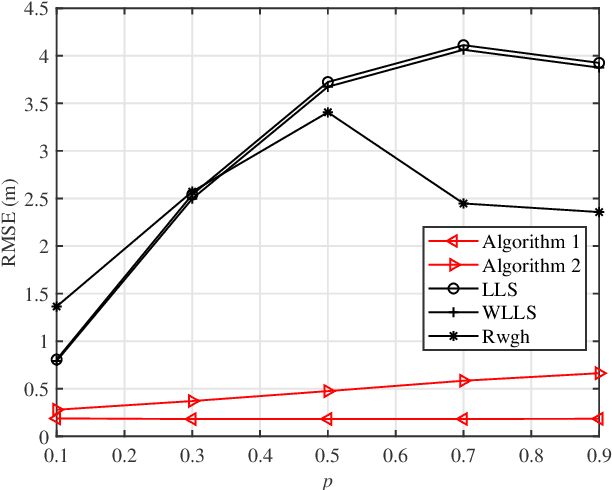
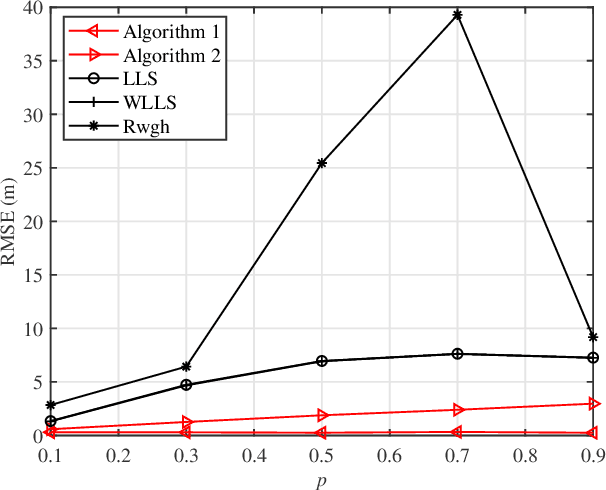
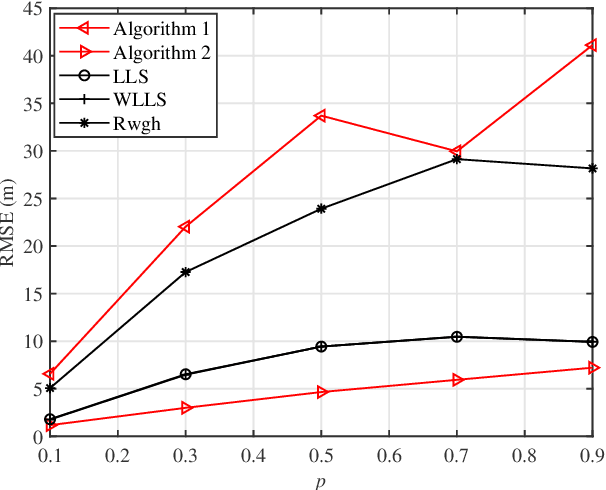
This paper proposes two efficient and easy-to-use error mitigation solutions to the problem of three-dimensional (3-D) angle-of-arrival (AOA) source localization in the mixed line-of-sight (LOS) and non-line-of-sight (NLOS) indoor environments. A weighted linear least squares estimator is derived first for the LOS AOA components in terms of the direction vectors of arrival, albeit in a sub-optimal manner. Next, data selection exploiting the sum of squared residuals is carried out to discard the error-prone NLOS connections. In so doing, the first approach is constituted and more accurate closed-form location estimates can be obtained. The second method applies a simulated annealing stochastic framework to realize the robust $\ell_1$-minimization criterion, which therefore falls into the methodology of statistical robustification. Computer simulations and ultrasonic onsite experiments are conducted to evaluate the performance of the two proposed methods, demonstrating their outstanding positioning results in the respective scenarios.