On the Role of Surrogates in Conformal Inference of Individual Causal Effects

Learning the Individual Treatment Effect (ITE) is essential for personalized decision making, yet causal inference has traditionally focused on aggregated treatment effects. While integrating conformal prediction with causal inference can provide valid uncertainty quantification for ITEs, the resulting prediction intervals are often excessively wide, limiting their practical utility. To address this limitation, we introduce \underline{S}urrogate-assisted \underline{C}onformal \underline{I}nference for \underline{E}fficient I\underline{N}dividual \underline{C}ausal \underline{E}ffects (SCIENCE), a framework designed to construct more efficient prediction intervals for ITEs. SCIENCE applies to various data configurations, including semi-supervised and surrogate-assisted semi-supervised learning. It accommodates covariate shifts between source data, which contain primary outcomes, and target data, which may include only surrogate outcomes or covariates. Leveraging semi-parametric efficiency theory, SCIENCE produces rate double-robust prediction intervals under mild rate convergence conditions, permitting the use of flexible non-parametric models to estimate nuisance functions. We quantify efficiency gains by comparing semi-parametric efficiency bounds with and without the incorporation of surrogates. Simulation studies demonstrate that our surrogate-assisted intervals offer substantial efficiency improvements over existing methods while maintaining valid group-conditional coverage. Applied to the phase 3 Moderna COVE COVID-19 vaccine trial, SCIENCE illustrates how multiple surrogate markers can be leveraged to generate more efficient prediction intervals.

Causal Customer Churn Analysis with Low-rank Tensor Block Hazard Model

This study introduces an innovative method for analyzing the impact of various interventions on customer churn, using the potential outcomes framework. We present a new causal model, the tensorized latent factor block hazard model, which incorporates tensor completion methods for a principled causal analysis of customer churn. A crucial element of our approach is the formulation of a 1-bit tensor completion for the parameter tensor. This captures hidden customer characteristics and temporal elements from churn records, effectively addressing the binary nature of churn data and its time-monotonic trends. Our model also uniquely categorizes interventions by their similar impacts, enhancing the precision and practicality of implementing customer retention strategies. For computational efficiency, we apply a projected gradient descent algorithm combined with spectral clustering. We lay down the theoretical groundwork for our model, including its non-asymptotic properties. The efficacy and superiority of our model are further validated through comprehensive experiments on both simulated and real-world applications.

Self-supervised Denoising via Low-rank Tensor Approximated Convolutional Neural Network

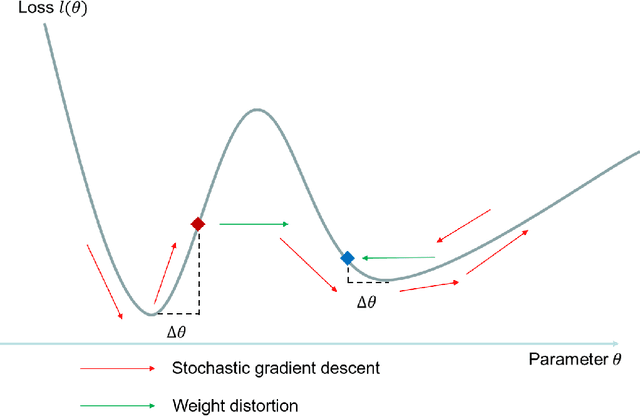
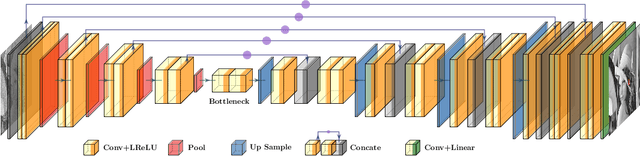
Noise is ubiquitous during image acquisition. Sufficient denoising is often an important first step for image processing. In recent decades, deep neural networks (DNNs) have been widely used for image denoising. Most DNN-based image denoising methods require a large-scale dataset or focus on supervised settings, in which single/pairs of clean images or a set of noisy images are required. This poses a significant burden on the image acquisition process. Moreover, denoisers trained on datasets of limited scale may incur over-fitting. To mitigate these issues, we introduce a new self-supervised framework for image denoising based on the Tucker low-rank tensor approximation. With the proposed design, we are able to characterize our denoiser with fewer parameters and train it based on a single image, which considerably improves the model generalizability and reduces the cost of data acquisition. Extensive experiments on both synthetic and real-world noisy images have been conducted. Empirical results show that our proposed method outperforms existing non-learning-based methods (e.g., low-pass filter, non-local mean), single-image unsupervised denoisers (e.g., DIP, NN+BM3D) evaluated on both in-sample and out-sample datasets. The proposed method even achieves comparable performances with some supervised methods (e.g., DnCNN).