Real-Time Safe Bipedal Robot Navigation using Linear Discrete Control Barrier Functions

Safe navigation in real-time is an essential task for humanoid robots in real-world deployment. Since humanoid robots are inherently underactuated thanks to unilateral ground contacts, a path is considered safe if it is obstacle-free and respects the robot's physical limitations and underlying dynamics. Existing approaches often decouple path planning from gait control due to the significant computational challenge caused by the full-order robot dynamics. In this work, we develop a unified, safe path and gait planning framework that can be evaluated online in real-time, allowing the robot to navigate clustered environments while sustaining stable locomotion. Our approach uses the popular Linear Inverted Pendulum (LIP) model as a template model to represent walking dynamics. It incorporates heading angles in the model to evaluate kinematic constraints essential for physically feasible gaits properly. In addition, we leverage discrete control barrier functions (DCBF) for obstacle avoidance, ensuring that the subsequent foot placement provides a safe navigation path within clustered environments. To guarantee real-time computation, we use a novel approximation of the DCBF to produce linear DCBF (LDCBF) constraints. We validate the proposed approach in simulation using a Digit robot in randomly generated environments. The results demonstrate that our approach can generate safe gaits for a non-trivial humanoid robot to navigate environments with randomly generated obstacles in real-time.

Unified Path and Gait Planning for Safe Bipedal Robot Navigation

Safe path and gait planning are essential for bipedal robots to navigate complex real-world environments. The prevailing approaches often plan the path and gait separately in a hierarchical fashion, potentially resulting in unsafe movements due to neglecting the physical constraints of walking robots. A safety-critical path must not only avoid obstacles but also ensure that the robot's gaits are subject to its dynamic and kinematic constraints. This work presents a novel approach that unifies path planning and gait planning via a Model Predictive Control (MPC) using the Linear Inverted Pendulum (LIP) model representing bipedal locomotion. This approach considers environmental constraints, such as obstacles, and the robot's kinematics and dynamics constraints. By using discrete-time Control Barrier Functions for obstacle avoidance, our approach generates the next foot landing position, ensuring robust walking gaits and a safe navigation path within clustered environments. We validated our proposed approach in simulation using a Digit robot in 20 randomly created environments. The results demonstrate improved performance in terms of safety and robustness when compared to hierarchical path and gait planning frameworks.

Safe Path Planning for Polynomial Shape Obstacles via Control Barrier Functions and Logistic Regression

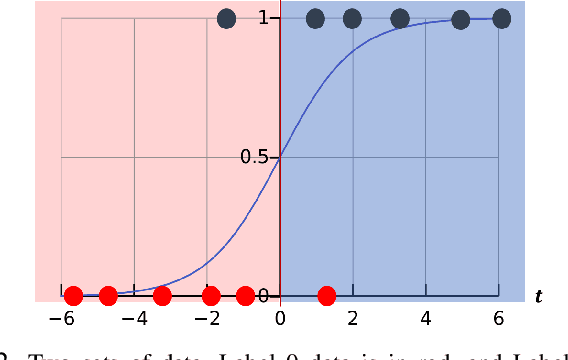
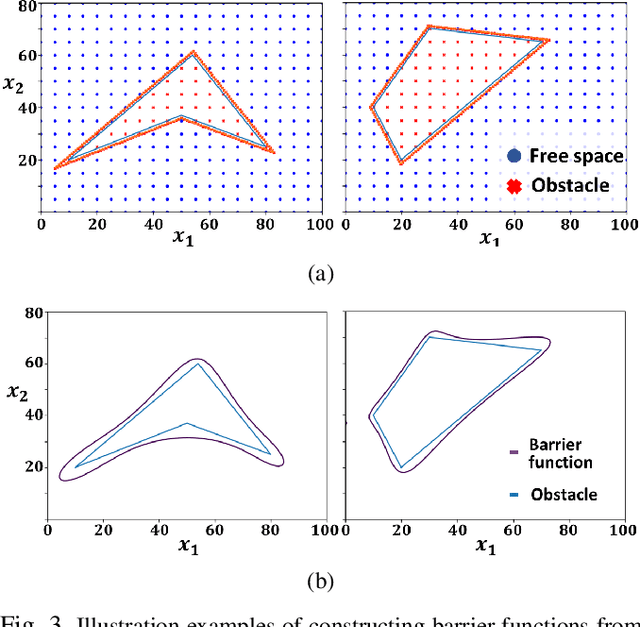
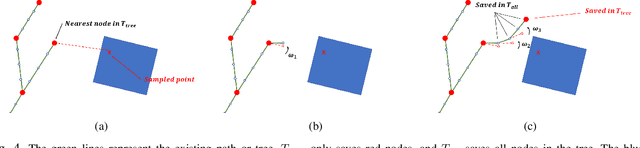
Safe path planning is critical for bipedal robots to operate in safety-critical environments. Common path planning algorithms, such as RRT or RRT*, typically use geometric or kinematic collision check algorithms to ensure collision-free paths toward the target position. However, such approaches may generate non-smooth paths that do not comply with the dynamics constraints of walking robots. It has been shown that the control barrier function (CBF) can be integrated with RRT/RRT* to synthesize dynamically feasible collision-free paths. Yet, existing work has been limited to simple circular or elliptical shape obstacles due to the challenging nature of constructing appropriate barrier functions to represent irregular-shaped obstacles. In this paper, we present a CBF-based RRT* algorithm for bipedal robots to generate a collision-free path through complex space with polynomial-shaped obstacles. In particular, we used logistic regression to construct polynomial barrier functions from a grid map of the environment to represent arbitrarily shaped obstacles. Moreover, we developed a multi-step CBF steering controller to ensure the efficiency of free space exploration. The proposed approach was first validated in simulation for a differential drive model, and then experimentally evaluated with a 3D humanoid robot, Digit, in a lab setting with randomly placed obstacles.