Detecting Zero-Day Attacks in Digital Substations via In-Context Learning

The occurrences of cyber attacks on the power grids have been increasing every year, with novel attack techniques emerging every year. In this paper, we address the critical challenge of detecting novel/zero-day attacks in digital substations that employ the IEC-61850 communication protocol. While many heuristic and machine learning (ML)-based methods have been proposed for attack detection in IEC-61850 digital substations, generalization to novel or zero-day attacks remains challenging. We propose an approach that leverages the in-context learning (ICL) capability of the transformer architecture, the fundamental building block of large language models. The ICL approach enables the model to detect zero-day attacks and learn from a few examples of that attack without explicit retraining. Our experiments on the IEC-61850 dataset demonstrate that the proposed method achieves more than $85\%$ detection accuracy on zero-day attacks while the existing state-of-the-art baselines fail. This work paves the way for building more secure and resilient digital substations of the future.

Fast Inverter Control by Learning the OPF Mapping using Sensitivity-Informed Gaussian Processes

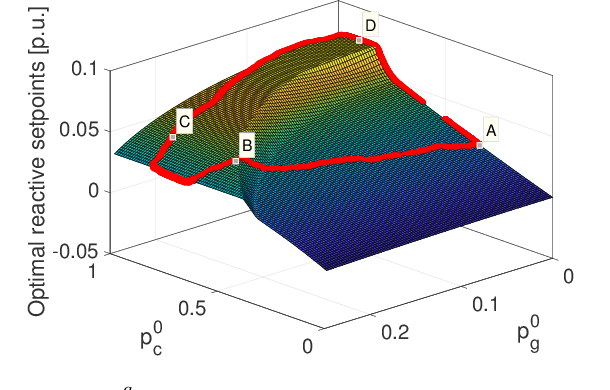
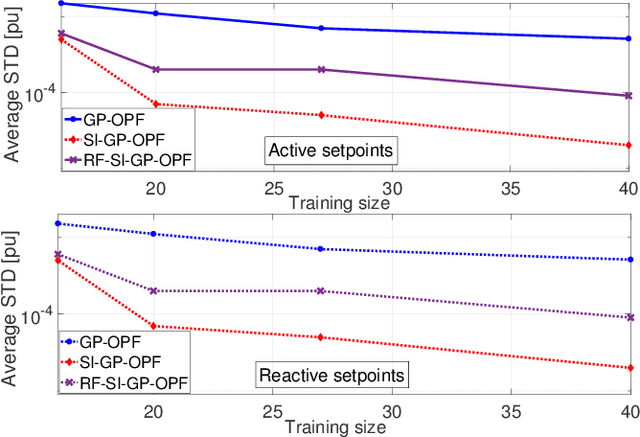
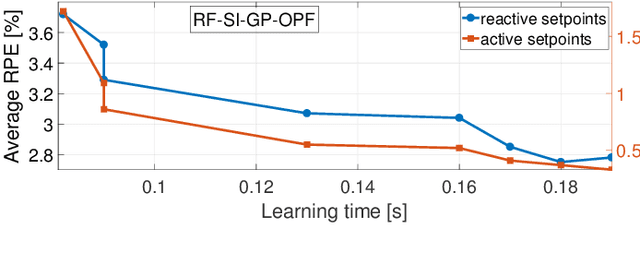
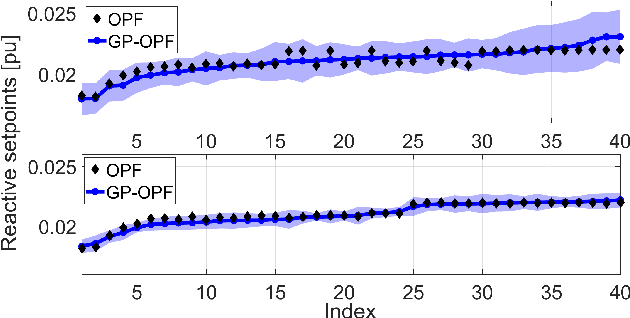
Fast inverter control is a desideratum towards the smoother integration of renewables. Adjusting inverter injection setpoints for distributed energy resources can be an effective grid control mechanism. However, finding such setpoints optimally requires solving an optimal power flow (OPF), which can be computationally taxing in real time. This work proposes learning the mapping from grid conditions to OPF minimizers using Gaussian processes (GPs). This GP-OPF model predicts inverter setpoints when presented with a new instance of grid conditions. Training enjoys closed-form expressions, and GP-OPF predictions come with confidence intervals. To improve upon data efficiency, we uniquely incorporate the sensitivities (partial derivatives) of the OPF mapping into GP-OPF. This expedites the process of generating a training dataset as fewer OPF instances need to be solved to attain the same accuracy. To further reduce computational efficiency, we approximate the kernel function of GP-OPF leveraging the concept of random features, which is neatly extended to sensitivity data. We perform sensitivity analysis for the second-order cone program (SOCP) relaxation of the OPF, whose sensitivities can be computed by merely solving a system of linear equations. Extensive numerical tests using real-world data on the IEEE 13- and 123-bus benchmark feeders corroborate the merits of GP-OPF.