Fast Inverter Control by Learning the OPF Mapping using Sensitivity-Informed Gaussian Processes

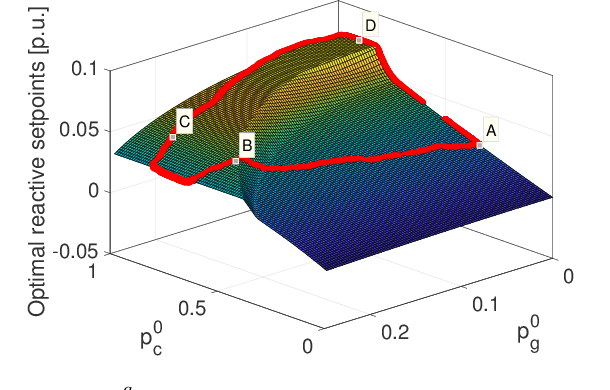
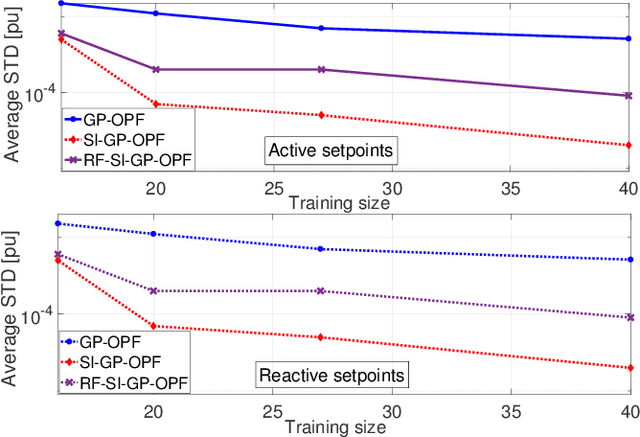
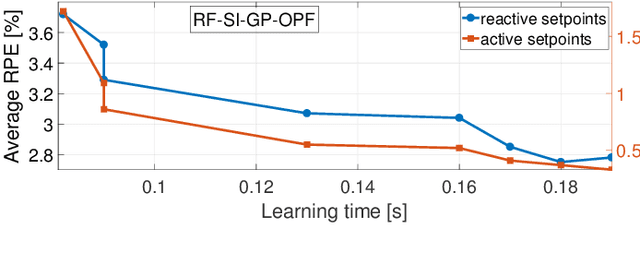
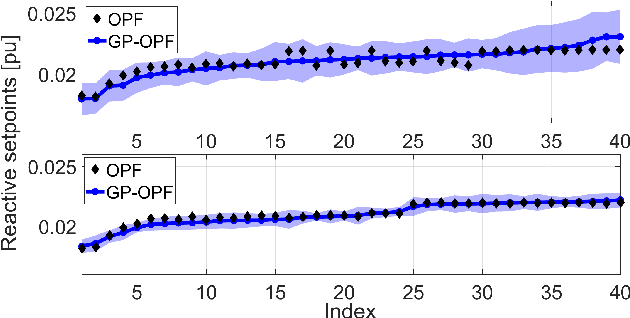
Fast inverter control is a desideratum towards the smoother integration of renewables. Adjusting inverter injection setpoints for distributed energy resources can be an effective grid control mechanism. However, finding such setpoints optimally requires solving an optimal power flow (OPF), which can be computationally taxing in real time. This work proposes learning the mapping from grid conditions to OPF minimizers using Gaussian processes (GPs). This GP-OPF model predicts inverter setpoints when presented with a new instance of grid conditions. Training enjoys closed-form expressions, and GP-OPF predictions come with confidence intervals. To improve upon data efficiency, we uniquely incorporate the sensitivities (partial derivatives) of the OPF mapping into GP-OPF. This expedites the process of generating a training dataset as fewer OPF instances need to be solved to attain the same accuracy. To further reduce computational efficiency, we approximate the kernel function of GP-OPF leveraging the concept of random features, which is neatly extended to sensitivity data. We perform sensitivity analysis for the second-order cone program (SOCP) relaxation of the OPF, whose sensitivities can be computed by merely solving a system of linear equations. Extensive numerical tests using real-world data on the IEEE 13- and 123-bus benchmark feeders corroborate the merits of GP-OPF.

Learning to Solve the AC-OPF using Sensitivity-Informed Deep Neural Networks

To shift the computational burden from real-time to offline in delay-critical power systems applications, recent works entertain the idea of using a deep neural network (DNN) to predict the solutions of the AC optimal power flow (AC-OPF) once presented load demands. As network topologies may change, training this DNN in a sample-efficient manner becomes a necessity. To improve data efficiency, this work utilizes the fact OPF data are not simple training labels, but constitute the solutions of a parametric optimization problem. We thus advocate training a sensitivity-informed DNN (SI-DNN) to match not only the OPF optimizers, but also their partial derivatives with respect to the OPF parameters (loads). It is shown that the required Jacobian matrices do exist under mild conditions, and can be readily computed from the related primal/dual solutions. The proposed SI-DNN is compatible with a broad range of OPF solvers, including a non-convex quadratically constrained quadratic program (QCQP), its semidefinite program (SDP) relaxation, and MATPOWER; while SI-DNN can be seamlessly integrated in other learning-to-OPF schemes. Numerical tests on three benchmark power systems corroborate the advanced generalization and constraint satisfaction capabilities for the OPF solutions predicted by an SI-DNN over a conventionally trained DNN, especially in low-data setups.