Semi-Supervised Metric Learning: A Deep Resurrection

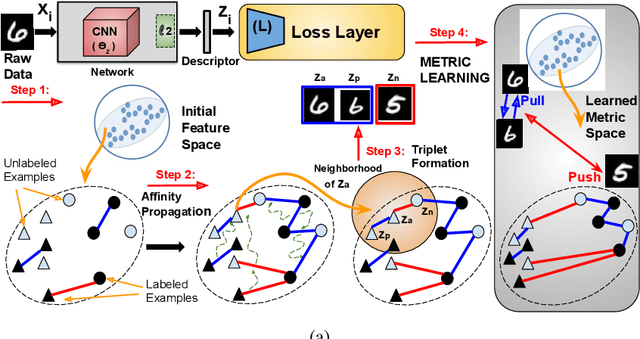
Distance Metric Learning (DML) seeks to learn a discriminative embedding where similar examples are closer, and dissimilar examples are apart. In this paper, we address the problem of Semi-Supervised DML (SSDML) that tries to learn a metric using a few labeled examples, and abundantly available unlabeled examples. SSDML is important because it is infeasible to manually annotate all the examples present in a large dataset. Surprisingly, with the exception of a few classical approaches that learn a linear Mahalanobis metric, SSDML has not been studied in the recent years, and lacks approaches in the deep SSDML scenario. In this paper, we address this challenging problem, and revamp SSDML with respect to deep learning. In particular, we propose a stochastic, graph-based approach that first propagates the affinities between the pairs of examples from labeled data, to that of the unlabeled pairs. The propagated affinities are used to mine triplet based constraints for metric learning. We impose orthogonality constraint on the metric parameters, as it leads to a better performance by avoiding a model collapse.

Unsupervised Deep Metric Learning via Orthogonality based Probabilistic Loss

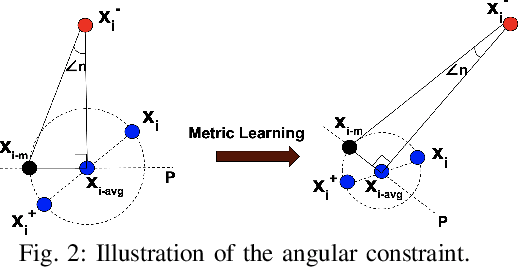
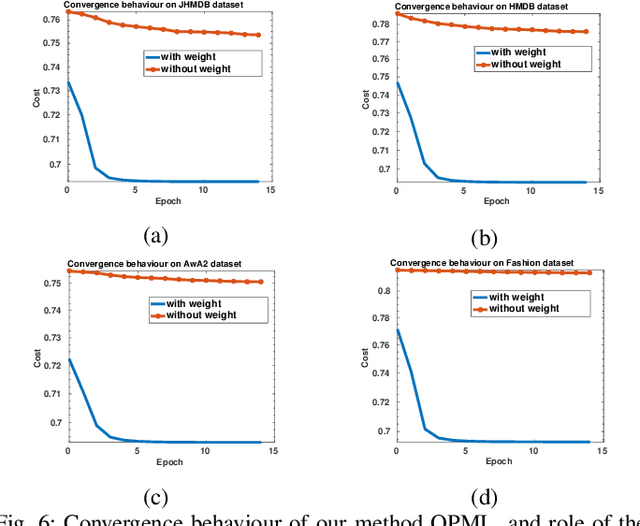
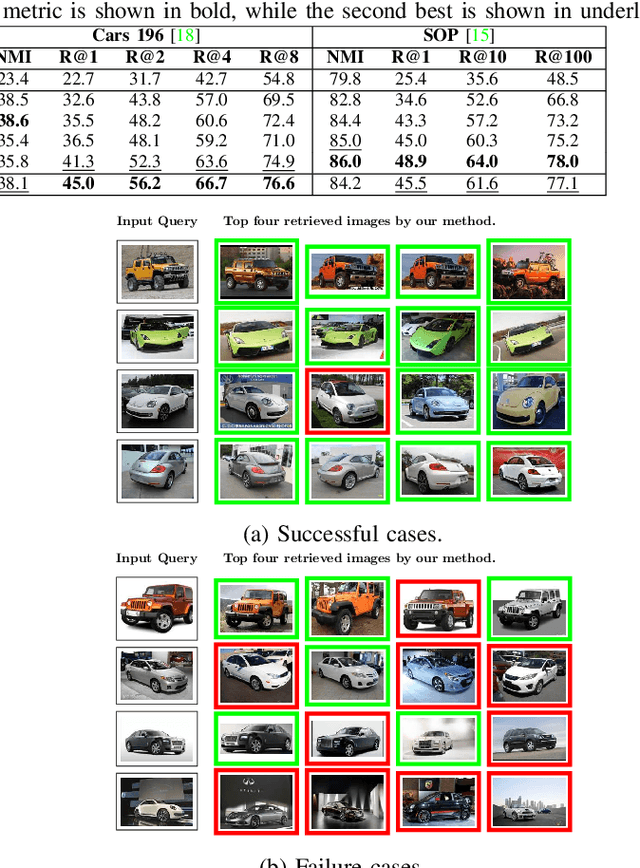
Metric learning is an important problem in machine learning. It aims to group similar examples together. Existing state-of-the-art metric learning approaches require class labels to learn a metric. As obtaining class labels in all applications is not feasible, we propose an unsupervised approach that learns a metric without making use of class labels. The lack of class labels is compensated by obtaining pseudo-labels of data using a graph-based clustering approach. The pseudo-labels are used to form triplets of examples, which guide the metric learning. We propose a probabilistic loss that minimizes the chances of each triplet violating an angular constraint. A weight function, and an orthogonality constraint in the objective speeds up the convergence and avoids a model collapse. We also provide a stochastic formulation of our method to scale up to large-scale datasets. Our studies demonstrate the competitiveness of our approach against state-of-the-art methods. We also thoroughly study the effect of the different components of our method.

Affinity guided Geometric Semi-Supervised Metric Learning

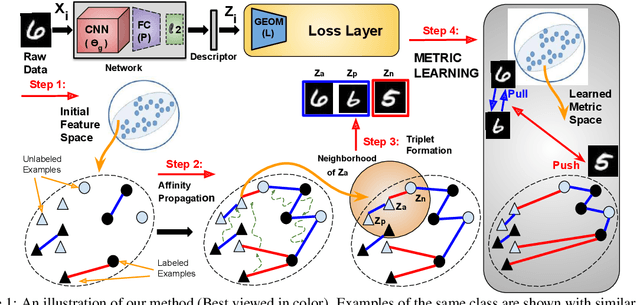
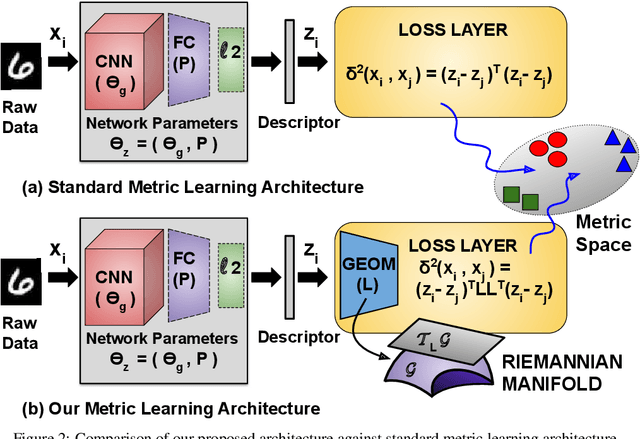
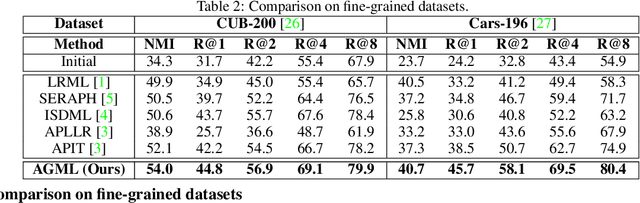
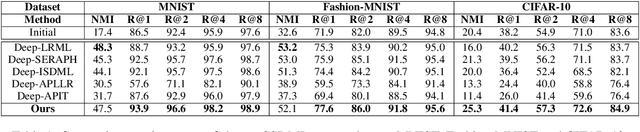
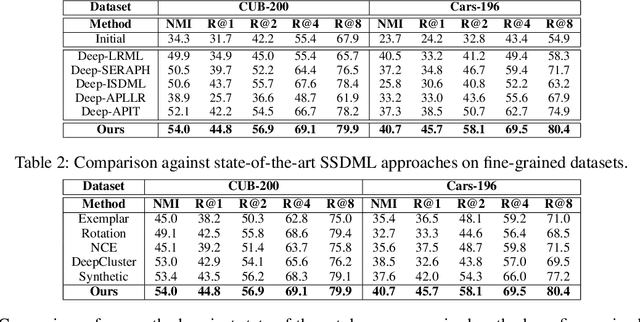
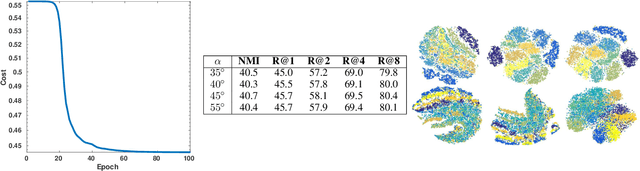
In this paper, we address the semi-supervised metric learning problem, where we learn a distance metric using very few labeled examples, and additionally available unlabeled data. To address the limitations of existing semi-supervised approaches, we integrate some of the best practices across metric learning, to achieve the state-of-the-art in the semi-supervised setting. In particular, we make use of a graph-based approach to propagate the affinities or similarities among the limited labeled pairs to the unlabeled data. Considering the neighborhood of an example, we take into account the propagated affinities to mine triplet constraints. An angular loss is imposed on these triplets to learn a metric. Additionally, we impose orthogonality on the parameters of the learned embedding to avoid a model collapse. In contrast to existing approaches, we propose a stochastic approach that scales well to large-scale datasets. We outperform various semi-supervised metric learning approaches on a number of benchmark datasets.