Affinity guided Geometric Semi-Supervised Metric Learning

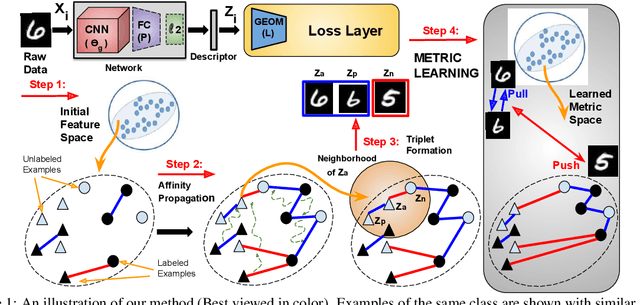
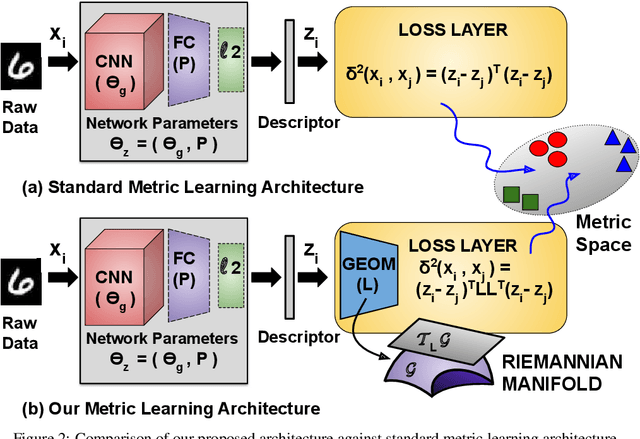
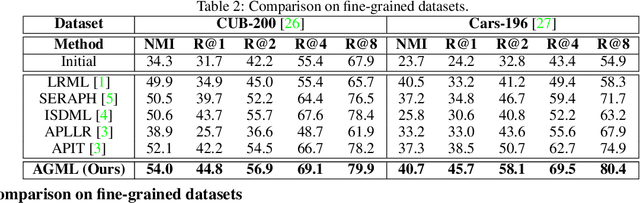
In this paper, we address the semi-supervised metric learning problem, where we learn a distance metric using very few labeled examples, and additionally available unlabeled data. To address the limitations of existing semi-supervised approaches, we integrate some of the best practices across metric learning, to achieve the state-of-the-art in the semi-supervised setting. In particular, we make use of a graph-based approach to propagate the affinities or similarities among the limited labeled pairs to the unlabeled data. Considering the neighborhood of an example, we take into account the propagated affinities to mine triplet constraints. An angular loss is imposed on these triplets to learn a metric. Additionally, we impose orthogonality on the parameters of the learned embedding to avoid a model collapse. In contrast to existing approaches, we propose a stochastic approach that scales well to large-scale datasets. We outperform various semi-supervised metric learning approaches on a number of benchmark datasets.