Deep Neural Networks Rival the Representation of Primate IT Cortex for Core Visual Object Recognition

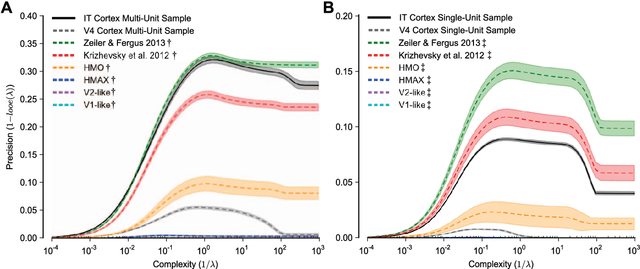
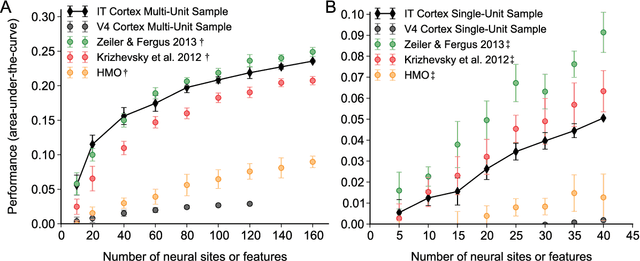
The primate visual system achieves remarkable visual object recognition performance even in brief presentations and under changes to object exemplar, geometric transformations, and background variation (a.k.a. core visual object recognition). This remarkable performance is mediated by the representation formed in inferior temporal (IT) cortex. In parallel, recent advances in machine learning have led to ever higher performing models of object recognition using artificial deep neural networks (DNNs). It remains unclear, however, whether the representational performance of DNNs rivals that of the brain. To accurately produce such a comparison, a major difficulty has been a unifying metric that accounts for experimental limitations such as the amount of noise, the number of neural recording sites, and the number trials, and computational limitations such as the complexity of the decoding classifier and the number of classifier training examples. In this work we perform a direct comparison that corrects for these experimental limitations and computational considerations. As part of our methodology, we propose an extension of "kernel analysis" that measures the generalization accuracy as a function of representational complexity. Our evaluations show that, unlike previous bio-inspired models, the latest DNNs rival the representational performance of IT cortex on this visual object recognition task. Furthermore, we show that models that perform well on measures of representational performance also perform well on measures of representational similarity to IT and on measures of predicting individual IT multi-unit responses. Whether these DNNs rely on computational mechanisms similar to the primate visual system is yet to be determined, but, unlike all previous bio-inspired models, that possibility cannot be ruled out merely on representational performance grounds.

The Neural Representation Benchmark and its Evaluation on Brain and Machine

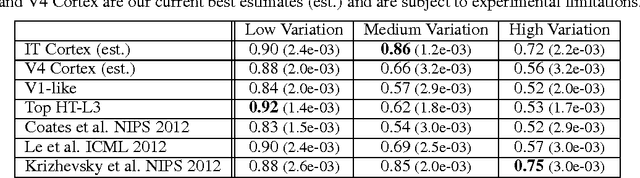
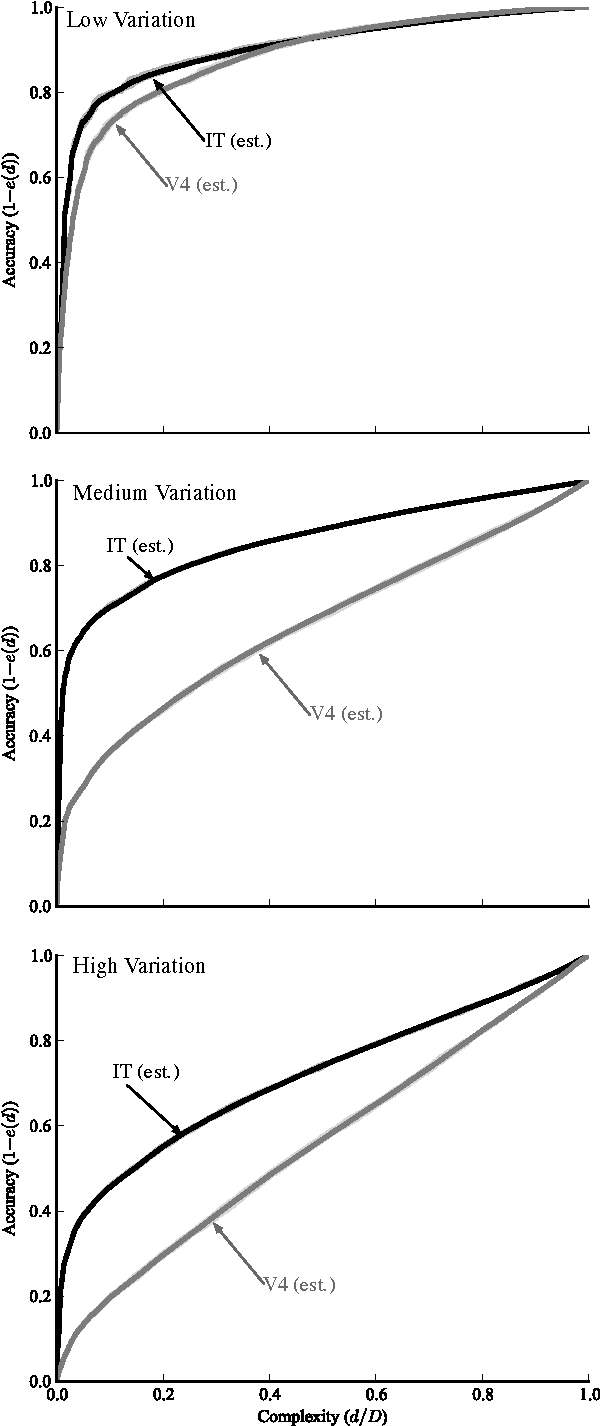
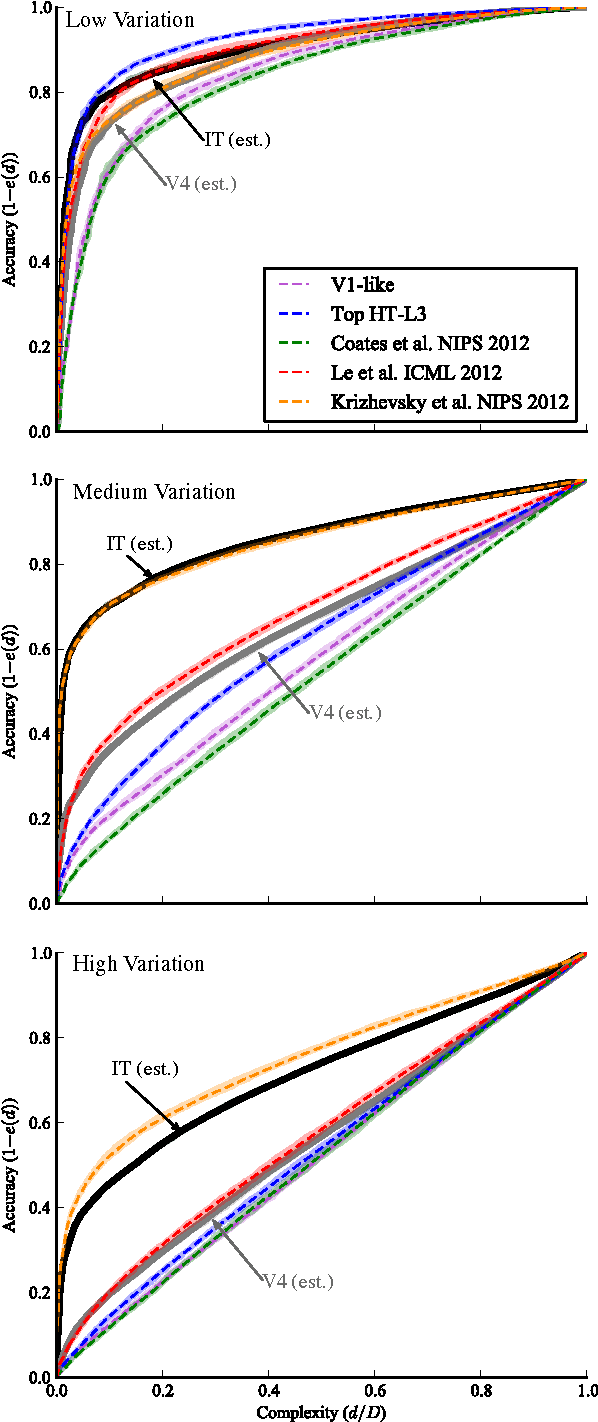
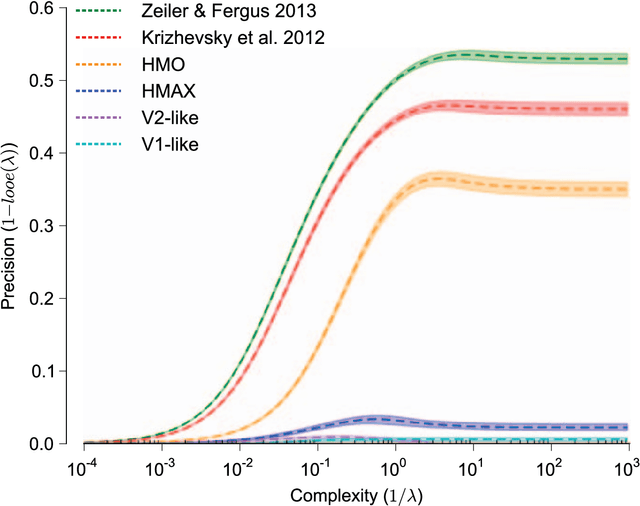
A key requirement for the development of effective learning representations is their evaluation and comparison to representations we know to be effective. In natural sensory domains, the community has viewed the brain as a source of inspiration and as an implicit benchmark for success. However, it has not been possible to directly test representational learning algorithms directly against the representations contained in neural systems. Here, we propose a new benchmark for visual representations on which we have directly tested the neural representation in multiple visual cortical areas in macaque (utilizing data from [Majaj et al., 2012]), and on which any computer vision algorithm that produces a feature space can be tested. The benchmark measures the effectiveness of the neural or machine representation by computing the classification loss on the ordered eigendecomposition of a kernel matrix [Montavon et al., 2011]. In our analysis we find that the neural representation in visual area IT is superior to visual area V4. In our analysis of representational learning algorithms, we find that three-layer models approach the representational performance of V4 and the algorithm in [Le et al., 2012] surpasses the performance of V4. Impressively, we find that a recent supervised algorithm [Krizhevsky et al., 2012] achieves performance comparable to that of IT for an intermediate level of image variation difficulty, and surpasses IT at a higher difficulty level. We believe this result represents a major milestone: it is the first learning algorithm we have found that exceeds our current estimate of IT representation performance. We hope that this benchmark will assist the community in matching the representational performance of visual cortex and will serve as an initial rallying point for further correspondence between representations derived in brains and machines.

Modeling Image Structure with Factorized Phase-Coupled Boltzmann Machines

We describe a model for capturing the statistical structure of local amplitude and local spatial phase in natural images. The model is based on a recently developed, factorized third-order Boltzmann machine that was shown to be effective at capturing higher-order structure in images by modeling dependencies among squared filter outputs (Ranzato and Hinton, 2010). Here, we extend this model to $L_p$-spherically symmetric subspaces. In order to model local amplitude and phase structure in images, we focus on the case of two dimensional subspaces, and the $L_2$-norm. When trained on natural images the model learns subspaces resembling quadrature-pair Gabor filters. We then introduce an additional set of hidden units that model the dependencies among subspace phases. These hidden units form a combinatorial mixture of phase coupling distributions, concentrated in the sum and difference of phase pairs. When adapted to natural images, these distributions capture local spatial phase structure in natural images.