Collaborative-Online-Learning-Enabled Distributionally Robust Motion Control for Multi-Robot Systems

This paper develops a novel COllaborative-Online-Learning (COOL)-enabled motion control framework for multi-robot systems to avoid collision amid randomly moving obstacles whose motion distributions are partially observable through decentralized data streams. To address the notable challenge of data acquisition due to occlusion, a COOL approach based on the Dirichlet process mixture model is proposed to efficiently extract motion distribution information by exchanging among robots selected learning structures. By leveraging the fine-grained local-moment information learned through COOL, a data-stream-driven ambiguity set for obstacle motion is constructed. We then introduce a novel ambiguity set propagation method, which theoretically admits the derivation of the ambiguity sets for obstacle positions over the entire prediction horizon by utilizing obstacle current positions and the ambiguity set for obstacle motion. Additionally, we develop a compression scheme with its safety guarantee to automatically adjust the complexity and granularity of the ambiguity set by aggregating basic ambiguity sets that are close in a measure space, thereby striking an attractive trade-off between control performance and computation time. Then the probabilistic collision-free trajectories are generated through distributionally robust optimization problems. The distributionally robust obstacle avoidance constraints based on the compressed ambiguity set are equivalently reformulated by deriving separating hyperplanes through tractable semi-definite programming. Finally, we establish the probabilistic collision avoidance guarantee and the long-term tracking performance guarantee for the proposed framework. The numerical simulations are used to demonstrate the efficacy and superiority of the proposed approach compared with state-of-the-art methods.

Differentiable Distributionally Robust Optimization Layers

In recent years, there has been a growing research interest in decision-focused learning, which embeds optimization problems as a layer in learning pipelines and demonstrates a superior performance than the prediction-focused approach. However, for distributionally robust optimization (DRO), a popular paradigm for decision-making under uncertainty, it is still unknown how to embed it as a layer, i.e., how to differentiate decisions with respect to an ambiguity set. In this paper, we develop such differentiable DRO layers for generic mixed-integer DRO problems with parameterized second-order conic ambiguity sets and discuss its extension to Wasserstein ambiguity sets. To differentiate the mixed-integer decisions, we propose a novel dual-view methodology by handling continuous and discrete parts of decisions via different principles. Specifically, we construct a differentiable energy-based surrogate to implement the dual-view methodology and use importance sampling to estimate its gradient. We further prove that such a surrogate enjoys the asymptotic convergency under regularization. As an application of the proposed differentiable DRO layers, we develop a novel decision-focused learning pipeline for contextual distributionally robust decision-making tasks and compare it with the prediction-focused approach in experiments.

Online Learning Based Risk-Averse Stochastic MPC of Constrained Linear Uncertain Systems

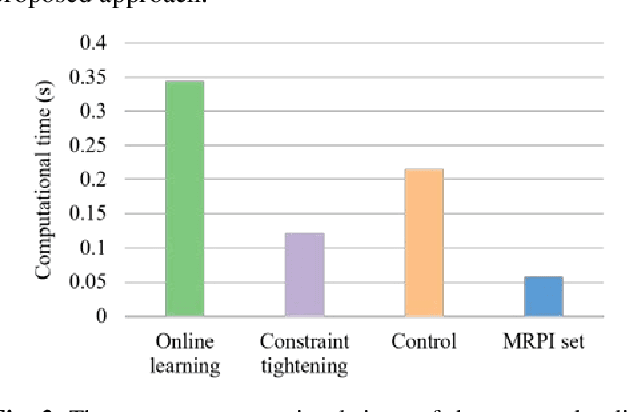
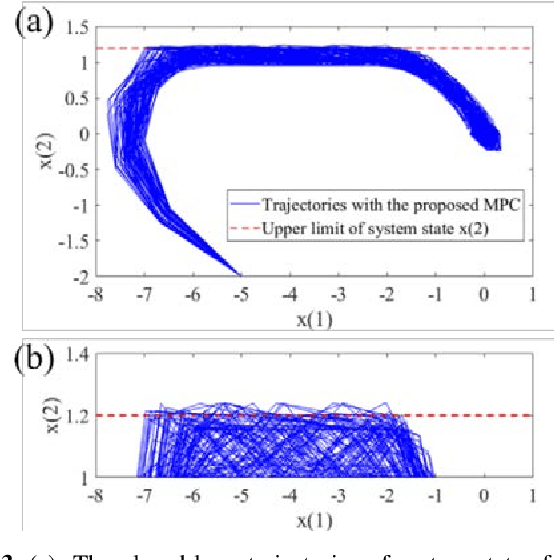
This paper investigates the problem of designing data-driven stochastic Model Predictive Control (MPC) for linear time-invariant systems under additive stochastic disturbance, whose probability distribution is unknown but can be partially inferred from data. We propose a novel online learning based risk-averse stochastic MPC framework in which Conditional Value-at-Risk (CVaR) constraints on system states are required to hold for a family of distributions called an ambiguity set. The ambiguity set is constructed from disturbance data by leveraging a Dirichlet process mixture model that is self-adaptive to the underlying data structure and complexity. Specifically, the structural property of multimodality is exploit-ed, so that the first- and second-order moment information of each mixture component is incorporated into the ambiguity set. A novel constraint tightening strategy is then developed based on an equivalent reformulation of distributionally ro-bust CVaR constraints over the proposed ambiguity set. As more data are gathered during the runtime of the controller, the ambiguity set is updated online using real-time disturbance data, which enables the risk-averse stochastic MPC to cope with time-varying disturbance distributions. The online variational inference algorithm employed does not require all collected data be learned from scratch, and therefore the proposed MPC is endowed with the guaranteed computational complexity of online learning. The guarantees on recursive feasibility and closed-loop stability of the proposed MPC are established via a safe update scheme. Numerical examples are used to illustrate the effectiveness and advantages of the proposed MPC.

Optimization under Uncertainty in the Era of Big Data and Deep Learning: When Machine Learning Meets Mathematical Programming

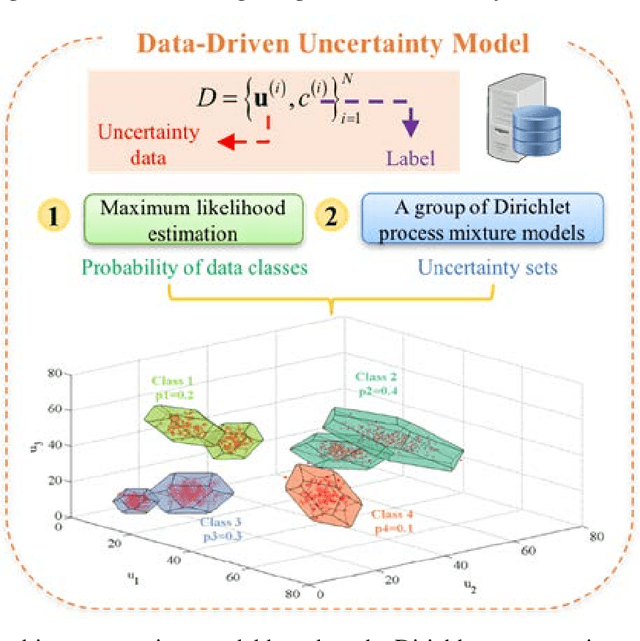
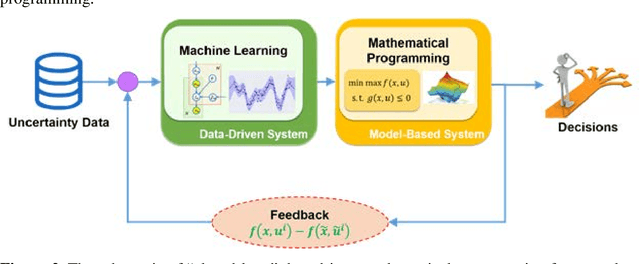
This paper reviews recent advances in the field of optimization under uncertainty via a modern data lens, highlights key research challenges and promise of data-driven optimization that organically integrates machine learning and mathematical programming for decision-making under uncertainty, and identifies potential research opportunities. A brief review of classical mathematical programming techniques for hedging against uncertainty is first presented, along with their wide spectrum of applications in Process Systems Engineering. A comprehensive review and classification of the relevant publications on data-driven distributionally robust optimization, data-driven chance constrained program, data-driven robust optimization, and data-driven scenario-based optimization is then presented. This paper also identifies fertile avenues for future research that focuses on a closed-loop data-driven optimization framework, which allows the feedback from mathematical programming to machine learning, as well as scenario-based optimization leveraging the power of deep learning techniques. Perspectives on online learning-based data-driven multistage optimization with a learning-while-optimizing scheme is presented.

Data-Driven Stochastic Robust Optimization: A General Computational Framework and Algorithm for Optimization under Uncertainty in the Big Data Era

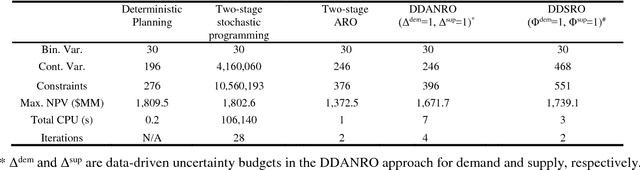
A novel data-driven stochastic robust optimization (DDSRO) framework is proposed for optimization under uncertainty leveraging labeled multi-class uncertainty data. Uncertainty data in large datasets are often collected from various conditions, which are encoded by class labels. Machine learning methods including Dirichlet process mixture model and maximum likelihood estimation are employed for uncertainty modeling. A DDSRO framework is further proposed based on the data-driven uncertainty model through a bi-level optimization structure. The outer optimization problem follows a two-stage stochastic programming approach to optimize the expected objective across different data classes; adaptive robust optimization is nested as the inner problem to ensure the robustness of the solution while maintaining computational tractability. A decomposition-based algorithm is further developed to solve the resulting multi-level optimization problem efficiently. Case studies on process network design and planning are presented to demonstrate the applicability of the proposed framework and algorithm.