Online Learning Based Risk-Averse Stochastic MPC of Constrained Linear Uncertain Systems
Paper and Code
Nov 20, 2020
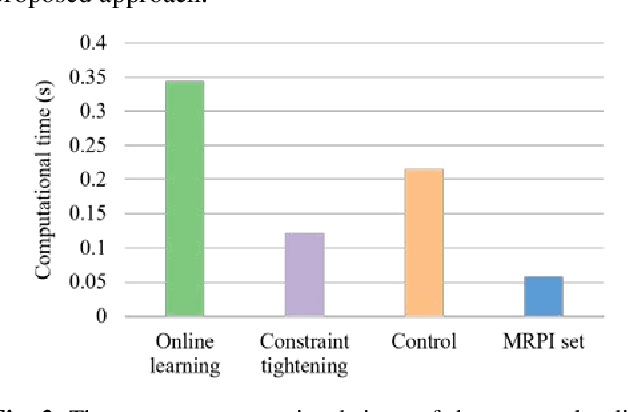
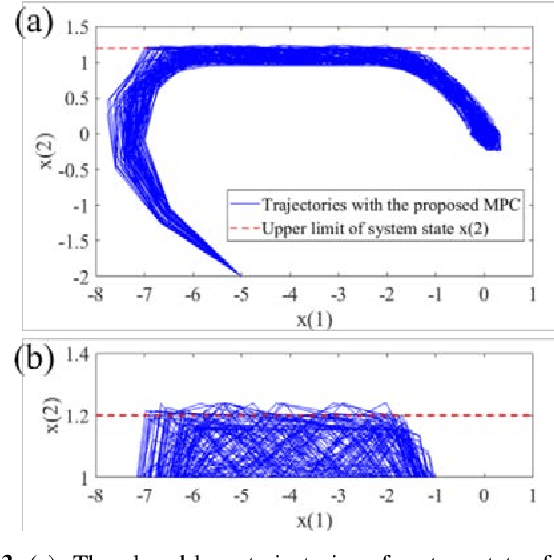

This paper investigates the problem of designing data-driven stochastic Model Predictive Control (MPC) for linear time-invariant systems under additive stochastic disturbance, whose probability distribution is unknown but can be partially inferred from data. We propose a novel online learning based risk-averse stochastic MPC framework in which Conditional Value-at-Risk (CVaR) constraints on system states are required to hold for a family of distributions called an ambiguity set. The ambiguity set is constructed from disturbance data by leveraging a Dirichlet process mixture model that is self-adaptive to the underlying data structure and complexity. Specifically, the structural property of multimodality is exploit-ed, so that the first- and second-order moment information of each mixture component is incorporated into the ambiguity set. A novel constraint tightening strategy is then developed based on an equivalent reformulation of distributionally ro-bust CVaR constraints over the proposed ambiguity set. As more data are gathered during the runtime of the controller, the ambiguity set is updated online using real-time disturbance data, which enables the risk-averse stochastic MPC to cope with time-varying disturbance distributions. The online variational inference algorithm employed does not require all collected data be learned from scratch, and therefore the proposed MPC is endowed with the guaranteed computational complexity of online learning. The guarantees on recursive feasibility and closed-loop stability of the proposed MPC are established via a safe update scheme. Numerical examples are used to illustrate the effectiveness and advantages of the proposed MPC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge