ARM: Role-Conditioned Neuron Transplantation for Training-Free Generalist LLM Agent Merging

Interactive large language model agents have advanced rapidly, but most remain specialized to a single environment and fail to adapt robustly to other environments. Model merging offers a training-free alternative by integrating multiple experts into a single model. In this paper, we propose Agent-Role Merging (ARM), an activation-guided, role-conditioned neuron transplantation method for model merging in LLM agents. ARM improves existing merging methods from static natural language tasks to multi-turn agent scenarios, and over the generalization ability across various interactive environments. This is achieved with a well designed 3-step framework: 1) constructing merged backbones, 2) selection based on its role-conditioned activation analysis, and 3) neuron transplantation for fine-grained refinements. Without gradient-based optimization, ARM improves cross-benchmark generalization while enjoying efficiency. Across diverse domains, the model obtained via ARM merging outperforms prior model merging methods and domain-specific expert models, while demonstrating strong out-of-domain generalization.

SCALER:Synthetic Scalable Adaptive Learning Environment for Reasoning

Reinforcement learning (RL) offers a principled way to enhance the reasoning capabilities of large language models, yet its effectiveness hinges on training signals that remain informative as models evolve. In practice, RL progress often slows when task difficulty becomes poorly aligned with model capability, or when training is dominated by a narrow set of recurring problem patterns. To jointly address these issues, we propose SCALER (Synthetic sCalable Adaptive Learning Environment for Reasoning), a framework that sustains effective learning signals through adaptive environment design. SCALER introduces a scalable synthesis pipeline that converts real-world programming problems into verifiable reasoning environments with controllable difficulty and unbounded instance generation, enabling RL training beyond finite datasets while preserving strong correctness guarantees. Building on this, SCALER further employs an adaptive multi-environment RL strategy that dynamically adjusts instance difficulty and curates the active set of environments to track the model's capability frontier and maintain distributional diversity. This co-adaptation prevents reward sparsity, mitigates overfitting to narrow task patterns, and supports sustained improvement throughout training. Extensive experiments show that SCALER consistently outperforms dataset-based RL baselines across diverse reasoning benchmarks and exhibits more stable, long-horizon training dynamics.

Long or short CoT? Investigating Instance-level Switch of Large Reasoning Models

With the rapid advancement of large reasoning models, long Chain-of-Thought (CoT) prompting has demonstrated strong performance on complex tasks. However, this often comes with a significant increase in token usage. In this paper, we conduct a comprehensive empirical analysis comparing long and short CoT strategies. Our findings reveal that while long CoT can lead to performance improvements, its benefits are often marginal relative to its significantly higher token consumption. Specifically, long CoT tends to outperform when ample generation budgets are available, whereas short CoT is more effective under tighter budget constraints. These insights underscore the need for a dynamic approach that selects the proper CoT strategy based on task context and resource availability. To address this, we propose SwitchCoT, an automatic framework that adaptively chooses between long and short CoT strategies to balance reasoning accuracy and computational efficiency. Moreover, SwitchCoT is designed to be budget-aware, making it broadly applicable across scenarios with varying resource constraints. Experimental results demonstrate that SwitchCoT can reduce inference costs by up to 50% while maintaining high accuracy. Notably, under limited token budgets, it achieves performance comparable to, or even exceeding, that of using either long or short CoT alone.

Knowledge Graph Embedding by Normalizing Flows

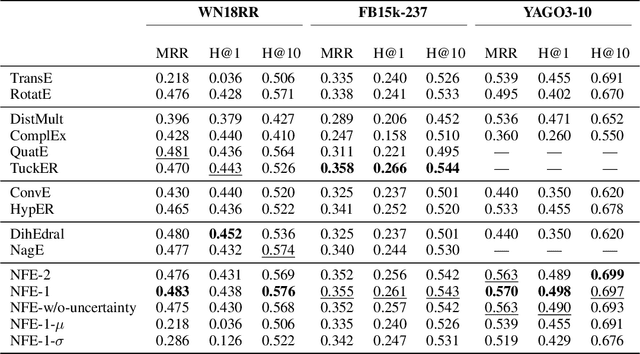
A key to knowledge graph embedding (KGE) is to choose a proper representation space, e.g., point-wise Euclidean space and complex vector space. In this paper, we propose a unified perspective of embedding and introduce uncertainty into KGE from the view of group theory. Our model can incorporate existing models (i.e., generality), ensure the computation is tractable (i.e., efficiency) and enjoy the expressive power of complex random variables (i.e., expressiveness). The core idea is that we embed entities/relations as elements of a symmetric group, i.e., permutations of a set. Permutations of different sets can reflect different properties of embedding. And the group operation of symmetric groups is easy to compute. In specific, we show that the embedding of many existing models, point vectors, can be seen as elements of a symmetric group. To reflect uncertainty, we first embed entities/relations as permutations of a set of random variables. A permutation can transform a simple random variable into a complex random variable for greater expressiveness, called a normalizing flow. We then define scoring functions by measuring the similarity of two normalizing flows, namely NFE. We construct several instantiating models and prove that they are able to learn logical rules. Experimental results demonstrate the effectiveness of introducing uncertainty and our model. The code is available at https://github.com/changyi7231/NFE.

Generative Flows with Matrix Exponential

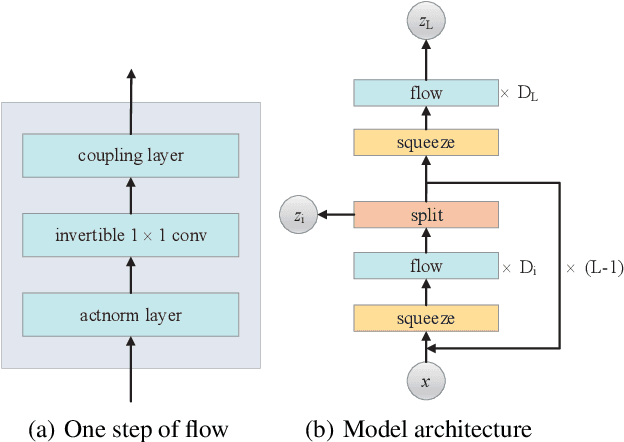
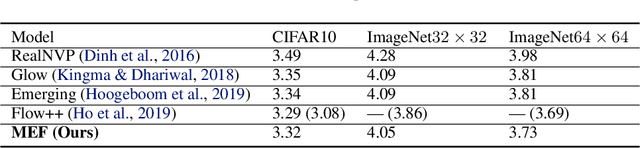
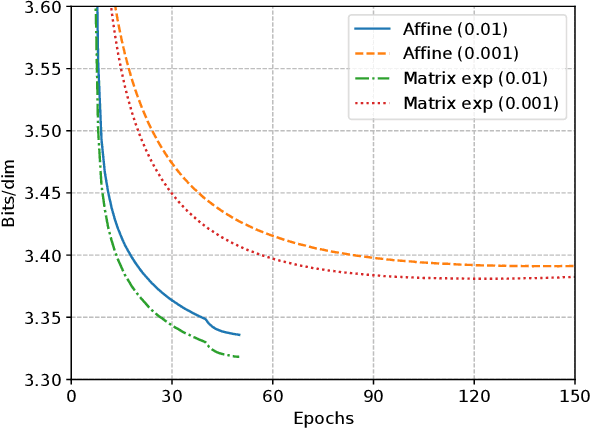
Generative flows models enjoy the properties of tractable exact likelihood and efficient sampling, which are composed of a sequence of invertible functions. In this paper, we incorporate matrix exponential into generative flows. Matrix exponential is a map from matrices to invertible matrices, this property is suitable for generative flows. Based on matrix exponential, we propose matrix exponential coupling layers that are a general case of affine coupling layers and matrix exponential invertible 1 x 1 convolutions that do not collapse during training. And we modify the networks architecture to make trainingstable andsignificantly speed up the training process. Our experiments show that our model achieves great performance on density estimation amongst generative flows models.