A multi-core periphery perspective: Ranking via relative centrality

Community and core-periphery are two widely studied graph structures, with their coexistence observed in real-world graphs (Rombach, Porter, Fowler \& Mucha [SIAM J. App. Math. 2014, SIAM Review 2017]). However, the nature of this coexistence is not well understood and has been pointed out as an open problem (Yanchenko \& Sengupta [Statistics Surveys, 2023]). Especially, the impact of inferring the core-periphery structure of a graph on understanding its community structure is not well utilized. In this direction, we introduce a novel quantification for graphs with ground truth communities, where each community has a densely connected part (the core), and the rest is more sparse (the periphery), with inter-community edges more frequent between the peripheries. Built on this structure, we propose a new algorithmic concept that we call relative centrality to detect the cores. We observe that core-detection algorithms based on popular centrality measures such as PageRank and degree centrality can show some bias in their outcome by selecting very few vertices from some cores. We show that relative centrality solves this bias issue and provide theoretical and simulation support, as well as experiments on real-world graphs. Core detection is known to have important applications with respect to core-periphery structures. In our model, we show a new application: relative-centrality-based algorithms can select a subset of the vertices such that it contains sufficient vertices from all communities, and points in this subset are better separable into their respective communities. We apply the methods to 11 biological datasets, with our methods resulting in a more balanced selection of vertices from all communities such that clustering algorithms have better performance on this set.

Confident Clustering via PCA Compression Ratio and Its Application to Single-cell RNA-seq Analysis

Unsupervised clustering algorithms for vectors has been widely used in the area of machine learning. Many applications, including the biological data we studied in this paper, contain some boundary datapoints which show combination properties of two underlying clusters and could lower the performance of the traditional clustering algorithms. We develop a confident clustering method aiming to diminish the influence of these datapoints and improve the clustering results. Concretely, for a list of datapoints, we give two clustering results. The first-round clustering attempts to classify only pure vectors with high confidence. Based on it, we classify more vectors with less confidence in the second round. We validate our algorithm on single-cell RNA-seq data, which is a powerful and widely used tool in biology area. Our confident clustering shows a high accuracy on our tested datasets. In addition, unlike traditional clustering methods in single-cell analysis, the confident clustering shows high stability under different choices of parameters.

Compressibility: Power of PCA in Clustering Problems Beyond Dimensionality Reduction

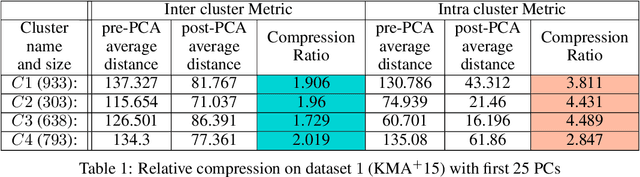
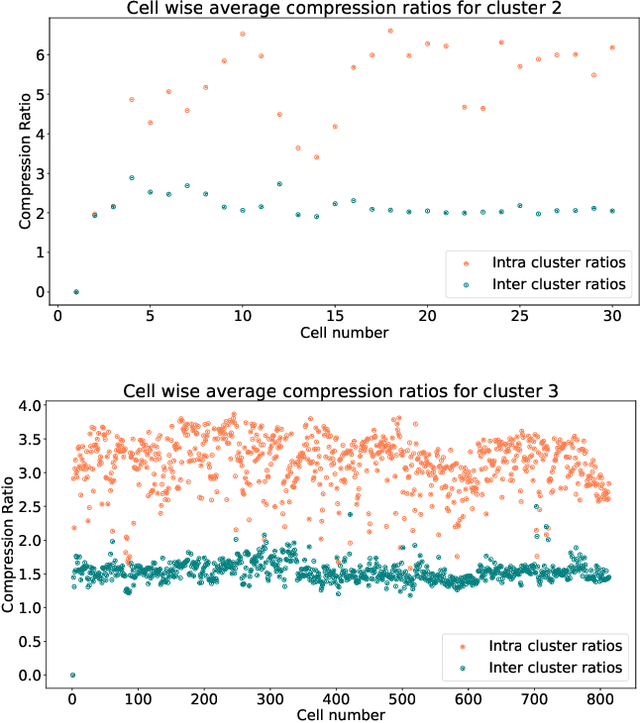
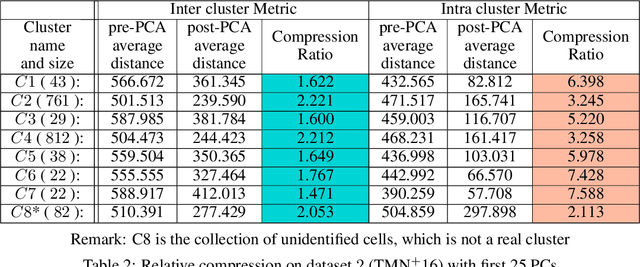
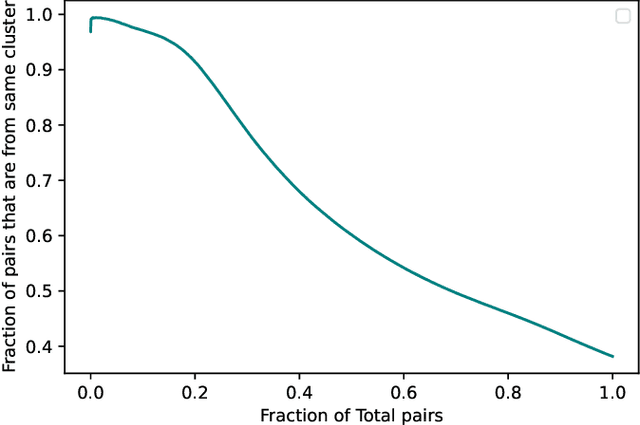
In this paper we take a step towards understanding the impact of principle component analysis (PCA) in the context of unsupervised clustering beyond a dimensionality reduction tool. We explore another property of PCA in vector clustering problems, which we call compressibility. This phenomenon shows that PCA significantly reduces the distance of data points belonging to the same clusters, while reducing inter-cluster distances relatively mildly. This gap explains many empirical observations found in practice. For example, in single-cell RNA-sequencing analysis, which is an application of vector clustering in biology, it has been observed that applying PCA on datasets significantly improves the accuracy of classical clustering algorithms such as K-means. We study this compression gap in both theory and practice. On the theoretical side, we analyze PCA in a fairly general probabilistic setup, which we call the random vector model. In terms of practice, we verify the compressibility of PCA on multiple single-cell RNA-seq datasets.

Recovering Unbalanced Communities in the Stochastic Block Model With Application to Clustering with a Faulty Oracle

The stochastic block model (SBM) is a fundamental model for studying graph clustering or community detection in networks. It has received great attention in the last decade and the balanced case, i.e., assuming all clusters have large size, has been well studied. However, our understanding of SBM with unbalanced communities (arguably, more relevant in practice) is still very limited. In this paper, we provide a simple SVD-based algorithm for recovering the communities in the SBM with communities of varying sizes. Under the KS-threshold conjecture, the tradeoff between the parameters in our algorithm is nearly optimal up to polylogarithmic factors for a wide range of regimes. As a byproduct, we obtain a time-efficient algorithm with improved query complexity for a clustering problem with a faulty oracle, which improves upon a number of previous work (Mazumdarand Saha [NIPS 2017], Larsen, Mitzenmacher and Tsourakakis [WWW 2020], Peng and Zhang[COLT 2021]). Under the KS-threshold conjecture, the query complexity of our algorithm is nearly optimal up to polylogarithmic factors.