Compressibility: Power of PCA in Clustering Problems Beyond Dimensionality Reduction

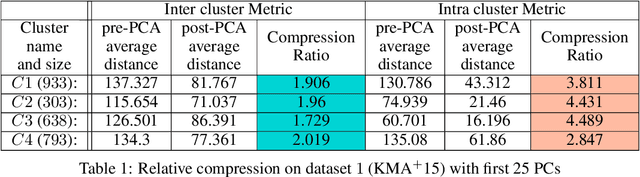
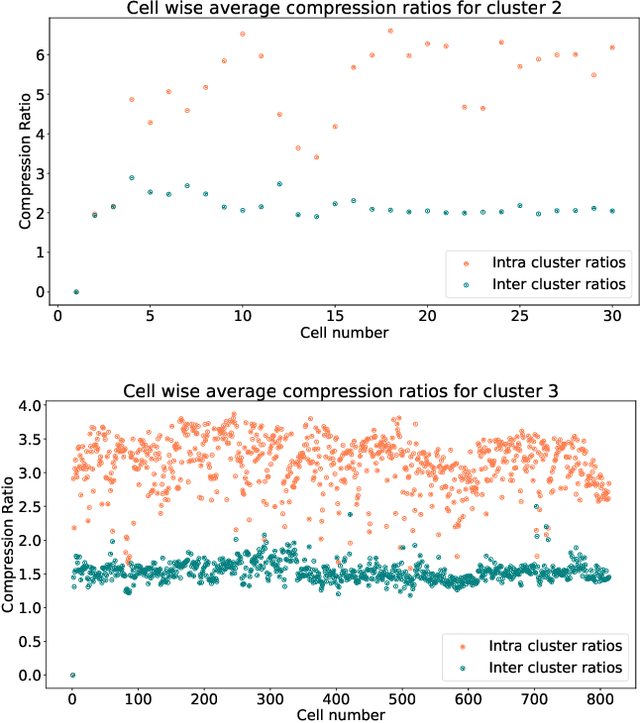
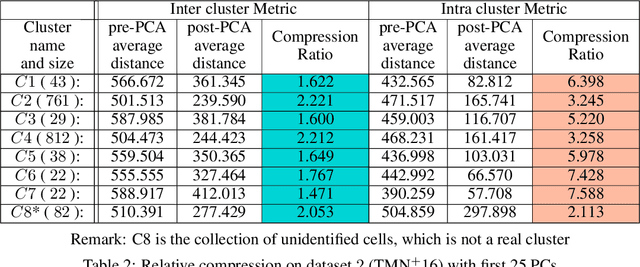
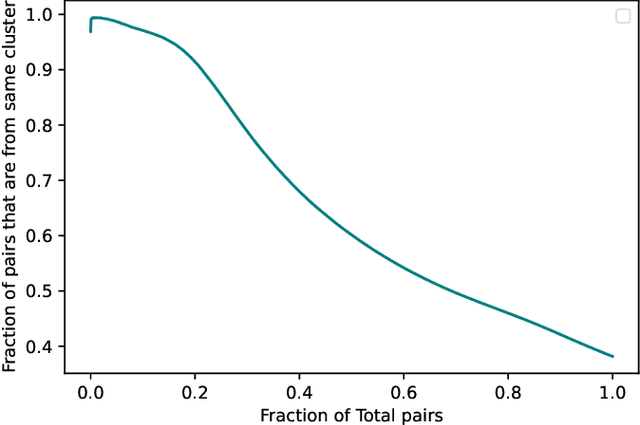
In this paper we take a step towards understanding the impact of principle component analysis (PCA) in the context of unsupervised clustering beyond a dimensionality reduction tool. We explore another property of PCA in vector clustering problems, which we call compressibility. This phenomenon shows that PCA significantly reduces the distance of data points belonging to the same clusters, while reducing inter-cluster distances relatively mildly. This gap explains many empirical observations found in practice. For example, in single-cell RNA-sequencing analysis, which is an application of vector clustering in biology, it has been observed that applying PCA on datasets significantly improves the accuracy of classical clustering algorithms such as K-means. We study this compression gap in both theory and practice. On the theoretical side, we analyze PCA in a fairly general probabilistic setup, which we call the random vector model. In terms of practice, we verify the compressibility of PCA on multiple single-cell RNA-seq datasets.