When Shift Happens - Confounding Is to Blame

Distribution shifts introduce uncertainty that undermines the robustness and generalization capabilities of machine learning models. While conventional wisdom suggests that learning causal-invariant representations enhances robustness to such shifts, recent empirical studies present a counterintuitive finding: (i) empirical risk minimization (ERM) can rival or even outperform state-of-the-art out-of-distribution (OOD) generalization methods, and (ii) its OOD generalization performance improves when all available covariates, not just causal ones, are utilized. Drawing on both empirical and theoretical evidence, we attribute this phenomenon to hidden confounding. Shifts in hidden confounding induce changes in data distributions that violate assumptions commonly made by existing OOD generalization approaches. Under such conditions, we prove that effective generalization requires learning environment-specific relationships, rather than relying solely on invariant ones. Furthermore, we show that models augmented with proxies for hidden confounders can mitigate the challenges posed by hidden confounding shifts. These findings offer new theoretical insights and practical guidance for designing robust OOD generalization algorithms and principled covariate selection strategies.

GNNs Getting ComFy: Community and Feature Similarity Guided Rewiring

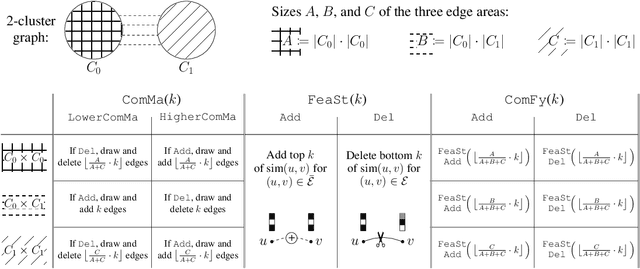
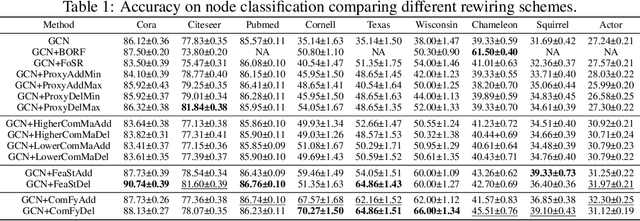
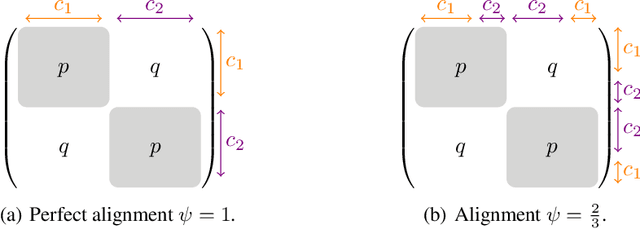
Maximizing the spectral gap through graph rewiring has been proposed to enhance the performance of message-passing graph neural networks (GNNs) by addressing over-squashing. However, as we show, minimizing the spectral gap can also improve generalization. To explain this, we analyze how rewiring can benefit GNNs within the context of stochastic block models. Since spectral gap optimization primarily influences community strength, it improves performance when the community structure aligns with node labels. Building on this insight, we propose three distinct rewiring strategies that explicitly target community structure, node labels, and their alignment: (a) community structure-based rewiring (ComMa), a more computationally efficient alternative to spectral gap optimization that achieves similar goals; (b) feature similarity-based rewiring (FeaSt), which focuses on maximizing global homophily; and (c) a hybrid approach (ComFy), which enhances local feature similarity while preserving community structure to optimize label-community alignment. Extensive experiments confirm the effectiveness of these strategies and support our theoretical insights.

Spectral Graph Pruning Against Over-Squashing and Over-Smoothing

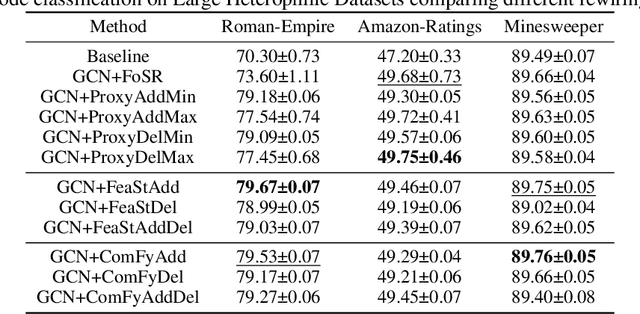
Message Passing Graph Neural Networks are known to suffer from two problems that are sometimes believed to be diametrically opposed: over-squashing and over-smoothing. The former results from topological bottlenecks that hamper the information flow from distant nodes and are mitigated by spectral gap maximization, primarily, by means of edge additions. However, such additions often promote over-smoothing that renders nodes of different classes less distinguishable. Inspired by the Braess phenomenon, we argue that deleting edges can address over-squashing and over-smoothing simultaneously. This insight explains how edge deletions can improve generalization, thus connecting spectral gap optimization to a seemingly disconnected objective of reducing computational resources by pruning graphs for lottery tickets. To this end, we propose a more effective spectral gap optimization framework to add or delete edges and demonstrate its effectiveness on large heterophilic datasets.