How many stations are sufficient? Exploring the effect of urban weather station density reduction on imputation accuracy of air temperature and humidity

Urban weather station networks (WSNs) are widely used to monitor urban weather and climate patterns and aid urban planning. However, maintaining WSNs is expensive and labor-intensive. Here, we present a step-wise station removal procedure to thin an existing WSN in Freiburg, Germany, and analyze the ability of WSN subsets to reproduce air temperature and humidity patterns of the entire original WSN for a year following a simulated reduction of WSN density. We found that substantial reductions in station numbers after one year of full deployment are possible while retaining high predictive accuracy. A reduction from 42 to 4 stations, for instance, increased mean prediction RMSEs from 0.69 K to 0.83 K for air temperature and from 3.8% to 4.4% for relative humidity, corresponding to RMSE increases of only 20% and 16%, respectively. Predictive accuracy is worse for remote stations in forests than for stations in built-up or open settings, but consistently better than a state-of-the-art numerical urban land-surface model (Surface Urban Energy and Water Balance Scheme). Stations located at the edges between built-up and rural areas are most valuable when reconstructing city-wide climate characteristics. Our study demonstrates the potential of thinning WSNs to maximize the efficient allocation of financial and personnel-related resources in urban climate research.

Advances in Land Surface Model-based Forecasting: A comparative study of LSTM, Gradient Boosting, and Feedforward Neural Network Models as prognostic state emulators

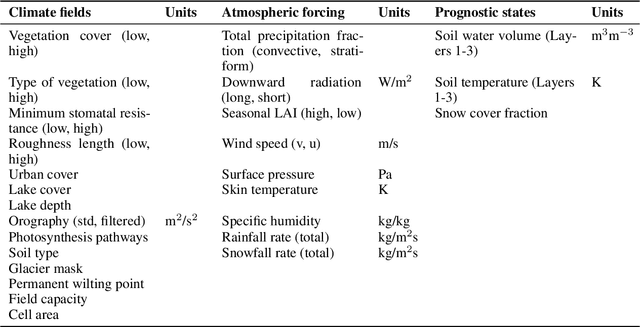
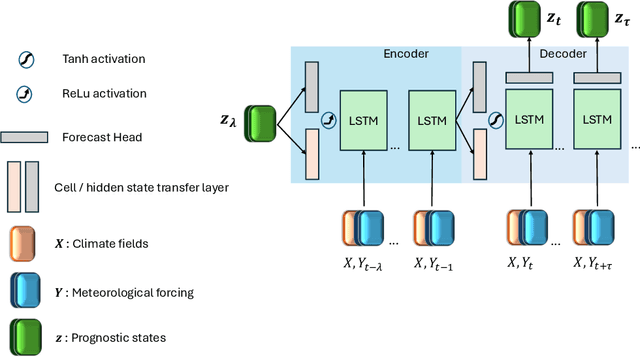
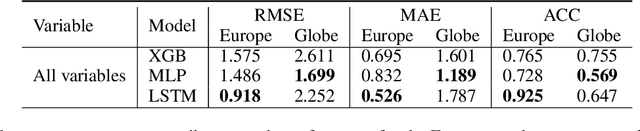
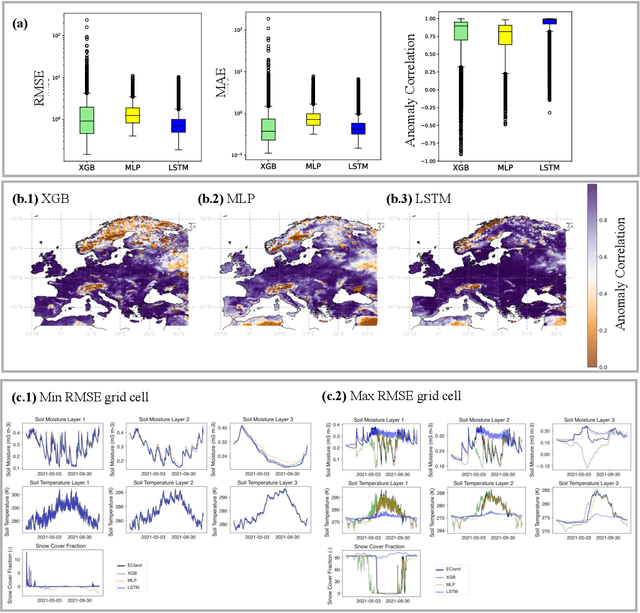
Most useful weather prediction for the public is near the surface. The processes that are most relevant for near-surface weather prediction are also those that are most interactive and exhibit positive feedback or have key role in energy partitioning. Land surface models (LSMs) consider these processes together with surface heterogeneity and forecast water, carbon and energy fluxes, and coupled with an atmospheric model provide boundary and initial conditions. This numerical parametrization of atmospheric boundaries being computationally expensive, statistical surrogate models are increasingly used to accelerated progress in experimental research. We evaluated the efficiency of three surrogate models in speeding up experimental research by simulating land surface processes, which are integral to forecasting water, carbon, and energy fluxes in coupled atmospheric models. Specifically, we compared the performance of a Long-Short Term Memory (LSTM) encoder-decoder network, extreme gradient boosting, and a feed-forward neural network within a physics-informed multi-objective framework. This framework emulates key states of the ECMWF's Integrated Forecasting System (IFS) land surface scheme, ECLand, across continental and global scales. Our findings indicate that while all models on average demonstrate high accuracy over the forecast period, the LSTM network excels in continental long-range predictions when carefully tuned, the XGB scores consistently high across tasks and the MLP provides an excellent implementation-time-accuracy trade-off. The runtime reduction achieved by the emulators in comparison to the full numerical models are significant, offering a faster, yet reliable alternative for conducting numerical experiments on land surfaces.

Computing AIC for black-box models using Generalised Degrees of Freedom: a comparison with cross-validation

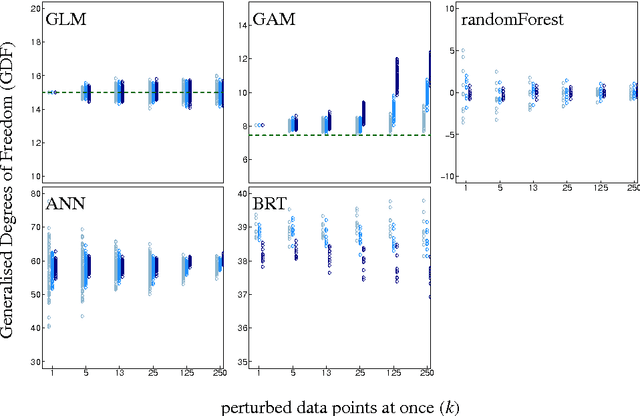
Generalised Degrees of Freedom (GDF), as defined by Ye (1998 JASA 93:120-131), represent the sensitivity of model fits to perturbations of the data. As such they can be computed for any statistical model, making it possible, in principle, to derive the number of parameters in machine-learning approaches. Defined originally for normally distributed data only, we here investigate the potential of this approach for Bernoulli-data. GDF-values for models of simulated and real data are compared to model complexity-estimates from cross-validation. Similarly, we computed GDF-based AICc for randomForest, neural networks and boosted regression trees and demonstrated its similarity to cross-validation. GDF-estimates for binary data were unstable and inconsistently sensitive to the number of data points perturbed simultaneously, while at the same time being extremely computer-intensive in their calculation. Repeated 10-fold cross-validation was more robust, based on fewer assumptions and faster to compute. Our findings suggest that the GDF-approach does not readily transfer to Bernoulli data and a wider range of regression approaches.