Computing AIC for black-box models using Generalised Degrees of Freedom: a comparison with cross-validation
Paper and Code
Mar 09, 2016

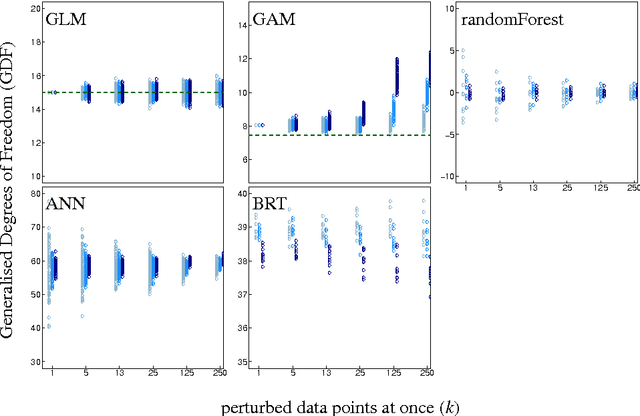

Generalised Degrees of Freedom (GDF), as defined by Ye (1998 JASA 93:120-131), represent the sensitivity of model fits to perturbations of the data. As such they can be computed for any statistical model, making it possible, in principle, to derive the number of parameters in machine-learning approaches. Defined originally for normally distributed data only, we here investigate the potential of this approach for Bernoulli-data. GDF-values for models of simulated and real data are compared to model complexity-estimates from cross-validation. Similarly, we computed GDF-based AICc for randomForest, neural networks and boosted regression trees and demonstrated its similarity to cross-validation. GDF-estimates for binary data were unstable and inconsistently sensitive to the number of data points perturbed simultaneously, while at the same time being extremely computer-intensive in their calculation. Repeated 10-fold cross-validation was more robust, based on fewer assumptions and faster to compute. Our findings suggest that the GDF-approach does not readily transfer to Bernoulli data and a wider range of regression approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge