Interpretable models for extrapolation in scientific machine learning

Data-driven models are central to scientific discovery. In efforts to achieve state-of-the-art model accuracy, researchers are employing increasingly complex machine learning algorithms that often outperform simple regressions in interpolative settings (e.g. random k-fold cross-validation) but suffer from poor extrapolation performance, portability, and human interpretability, which limits their potential for facilitating novel scientific insight. Here we examine the trade-off between model performance and interpretability across a broad range of science and engineering problems with an emphasis on materials science datasets. We compare the performance of black box random forest and neural network machine learning algorithms to that of single-feature linear regressions which are fitted using interpretable input features discovered by a simple random search algorithm. For interpolation problems, the average prediction errors of linear regressions were twice as high as those of black box models. Remarkably, when prediction tasks required extrapolation, linear models yielded average error only 5% higher than that of black box models, and outperformed black box models in roughly 40% of the tested prediction tasks, which suggests that they may be desirable over complex algorithms in many extrapolation problems because of their superior interpretability, computational overhead, and ease of use. The results challenge the common assumption that extrapolative models for scientific machine learning are constrained by an inherent trade-off between performance and interpretability.

ACED: Accelerated Computational Electrochemical systems Discovery

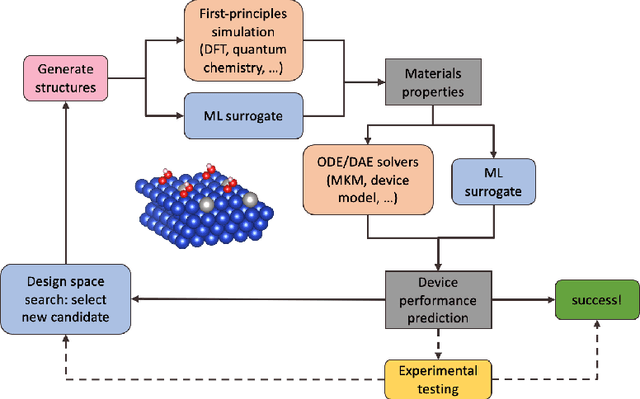
Large-scale electrification is vital to addressing the climate crisis, but many engineering challenges remain to fully electrifying both the chemical industry and transportation. In both of these areas, new electrochemical materials and systems will be critical, but developing these systems currently relies heavily on computationally expensive first-principles simulations as well as human-time-intensive experimental trial and error. We propose to develop an automated workflow that accelerates these computational steps by introducing both automated error handling in generating the first-principles training data as well as physics-informed machine learning surrogates to further reduce computational cost. It will also have the capacity to include automated experiments "in the loop" in order to dramatically accelerate the overall materials discovery pipeline.

Machine-learned metrics for predicting the likelihood of success in materials discovery

Materials discovery is often compared to the challenge of finding a needle in a haystack. While much work has focused on accurately predicting the properties of candidate materials with machine learning (ML), which amounts to evaluating whether a given candidate is a piece of straw or a needle, less attention has been paid to a critical question: Are we searching in the right haystack? We refer to the haystack as the design space for a particular materials discovery problem (i.e. the set of possible candidate materials to synthesize), and thus frame this question as one of design space selection. In this paper, we introduce two metrics, the Predicted Fraction of Improved Candidates (PFIC), and the Cumulative Maximum Likelihood of Improvement (CMLI), which we demonstrate can identify discovery-rich and discovery-poor design spaces, respectively. Using CMLI and PFIC together to identify optimal design spaces can significantly accelerate ML-driven materials discovery.

Overcoming data scarcity with transfer learning

Despite increasing focus on data publication and discovery in materials science and related fields, the global view of materials data is highly sparse. This sparsity encourages training models on the union of multiple datasets, but simple unions can prove problematic as (ostensibly) equivalent properties may be measured or computed differently depending on the data source. These hidden contextual differences introduce irreducible errors into analyses, fundamentally limiting their accuracy. Transfer learning, where information from one dataset is used to inform a model on another, can be an effective tool for bridging sparse data while preserving the contextual differences in the underlying measurements. Here, we describe and compare three techniques for transfer learning: multi-task, difference, and explicit latent variable architectures. We show that difference architectures are most accurate in the multi-fidelity case of mixed DFT and experimental band gaps, while multi-task most improves classification performance of color with band gaps. For activation energies of steps in NO reduction, the explicit latent variable method is not only the most accurate, but also enjoys cancellation of errors in functions that depend on multiple tasks. These results motivate the publication of high quality materials datasets that encode transferable information, independent of industrial or academic interest in the particular labels, and encourage further development and application of transfer learning methods to materials informatics problems.

Building Data-driven Models with Microstructural Images: Generalization and Interpretability

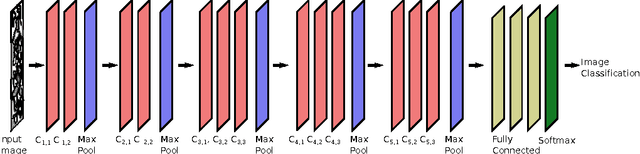
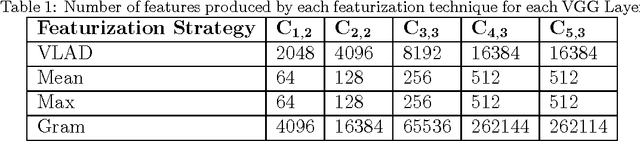
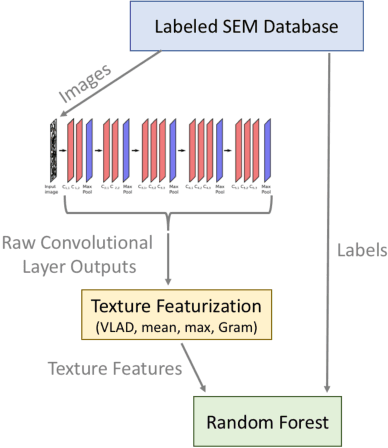
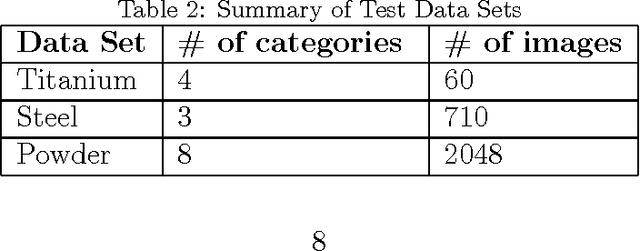
As data-driven methods rise in popularity in materials science applications, a key question is how these machine learning models can be used to understand microstructure. Given the importance of process-structure-property relations throughout materials science, it seems logical that models that can leverage microstructural data would be more capable of predicting property information. While there have been some recent attempts to use convolutional neural networks to understand microstructural images, these early studies have focused only on which featurizations yield the highest machine learning model accuracy for a single data set. This paper explores the use of convolutional neural networks for classifying microstructure with a more holistic set of objectives in mind: generalization between data sets, number of features required, and interpretability.

High-Dimensional Materials and Process Optimization using Data-driven Experimental Design with Well-Calibrated Uncertainty Estimates

The optimization of composition and processing to obtain materials that exhibit desirable characteristics has historically relied on a combination of scientist intuition, trial and error, and luck. We propose a methodology that can accelerate this process by fitting data-driven models to experimental data as it is collected to suggest which experiment should be performed next. This methodology can guide the scientist to test the most promising candidates earlier, and can supplement scientific intuition and knowledge with data-driven insights. A key strength of the proposed framework is that it scales to high-dimensional parameter spaces, as are typical in materials discovery applications. Importantly, the data-driven models incorporate uncertainty analysis, so that new experiments are proposed based on a combination of exploring high-uncertainty candidates and exploiting high-performing regions of parameter space. Over four materials science test cases, our methodology led to the optimal candidate being found with three times fewer required measurements than random guessing on average.