Toward Generalizable Whole Brain Representations with High-Resolution Light-Sheet Data

Unprecedented visual details of biological structures are being revealed by subcellular-resolution whole-brain 3D microscopy data, enabled by recent advances in intact tissue processing and light-sheet fluorescence microscopy (LSFM). These volumetric data offer rich morphological and spatial cellular information, however, the lack of scalable data processing and analysis methods tailored to these petabyte-scale data poses a substantial challenge for accurate interpretation. Further, existing models for visual tasks such as object detection and classification struggle to generalize to this type of data. To accelerate the development of suitable methods and foundational models, we present CANVAS, a comprehensive set of high-resolution whole mouse brain LSFM benchmark data, encompassing six neuronal and immune cell-type markers, along with cell annotations and a leaderboard. We also demonstrate challenges in generalization of baseline models built on existing architectures, especially due to the heterogeneity in cellular morphology across phenotypes and anatomical locations in the brain. To the best of our knowledge, CANVAS is the first and largest LSFM benchmark that captures intact mouse brain tissue at subcellular level, and includes extensive annotations of cells throughout the brain.

Navigating the Dynamics of Financial Embeddings over Time

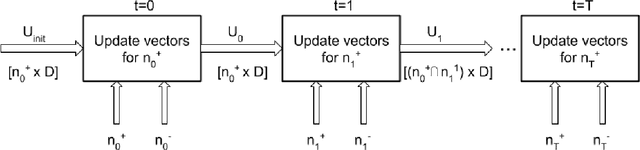
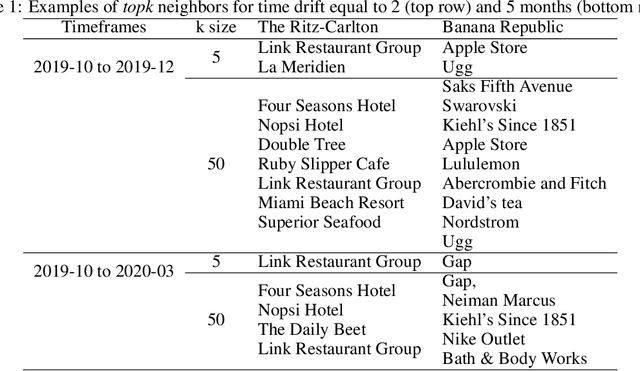
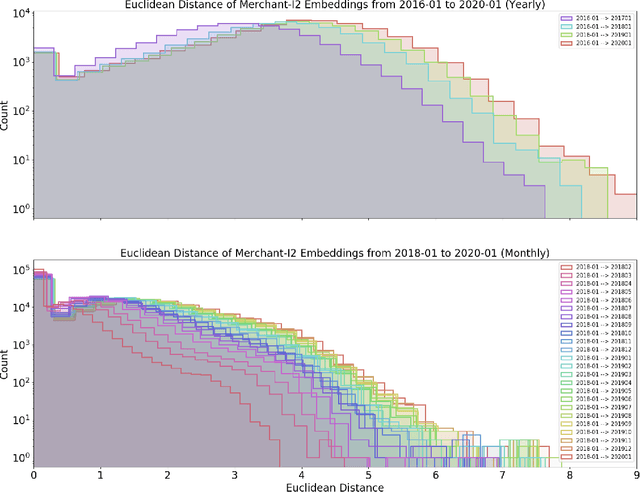
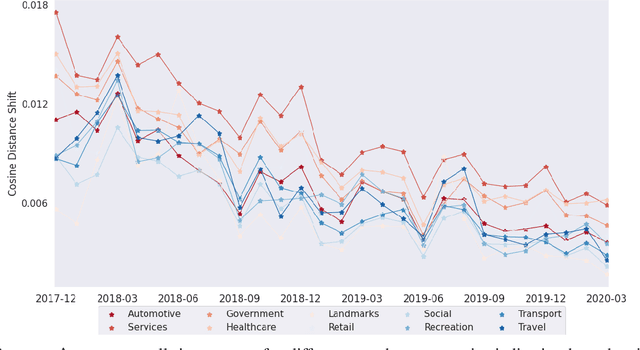
Financial transactions constitute connections between entities and through these connections a large scale heterogeneous weighted graph is formulated. In this labyrinth of interactions that are continuously updated, there exists a variety of similarity-based patterns that can provide insights into the dynamics of the financial system. With the current work, we propose the application of Graph Representation Learning in a scalable dynamic setting as a means of capturing these patterns in a meaningful and robust way. We proceed to perform a rigorous qualitative analysis of the latent trajectories to extract real world insights from the proposed representations and their evolution over time that is to our knowledge the first of its kind in the financial sector. Shifts in the latent space are associated with known economic events and in particular the impact of the recent Covid-19 pandemic to consumer patterns. Capturing such patterns indicates the value added to financial modeling through the incorporation of latent graph representations.

Quantifying Challenges in the Application of Graph Representation Learning

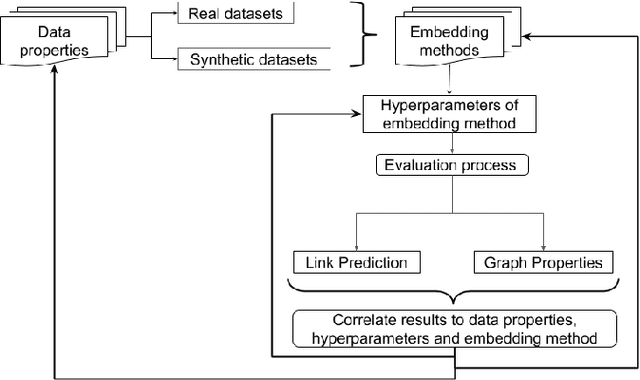
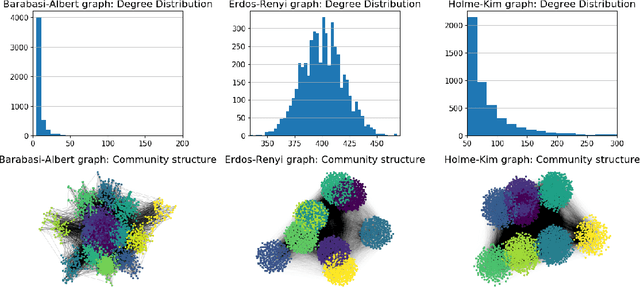
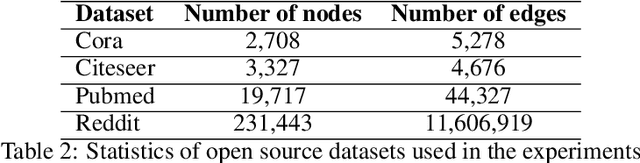
Graph Representation Learning (GRL) has experienced significant progress as a means to extract structural information in a meaningful way for subsequent learning tasks. Current approaches including shallow embeddings and Graph Neural Networks have mostly been tested with node classification and link prediction tasks. In this work, we provide an application oriented perspective to a set of popular embedding approaches and evaluate their representational power with respect to real-world graph properties. We implement an extensive empirical data-driven framework to challenge existing norms regarding the expressive power of embedding approaches in graphs with varying patterns along with a theoretical analysis of the limitations we discovered in this process. Our results suggest that "one-to-fit-all" GRL approaches are hard to define in real-world scenarios and as new methods are being introduced they should be explicit about their ability to capture graph properties and their applicability in datasets with non-trivial structural differences.