pmuBAGE: The Benchmarking Assortment of Generated PMU Data for Power System Events

This paper introduces pmuGE (phasor measurement unit Generator of Events), one of the first data-driven generative model for power system event data. We have trained this model on thousands of actual events and created a dataset denoted pmuBAGE (the Benchmarking Assortment of Generated PMU Events). The dataset consists of almost 1000 instances of labeled event data to encourage benchmark evaluations on phasor measurement unit (PMU) data analytics. PMU data are challenging to obtain, especially those covering event periods. Nevertheless, power system problems have recently seen phenomenal advancements via data-driven machine learning solutions. A highly accessible standard benchmarking dataset would enable a drastic acceleration of the development of successful machine learning techniques in this field. We propose a novel learning method based on the Event Participation Decomposition of Power System Events, which makes it possible to learn a generative model of PMU data during system anomalies. The model can create highly realistic event data without compromising the differential privacy of the PMUs used to train it. The dataset is available online for any researcher or practitioner to use at the pmuBAGE Github Repository: https://github.com/NanpengYu/pmuBAGE.

pmuBAGE: The Benchmarking Assortment of Generated PMU Data for Power System Events -- Part I: Overview and Results

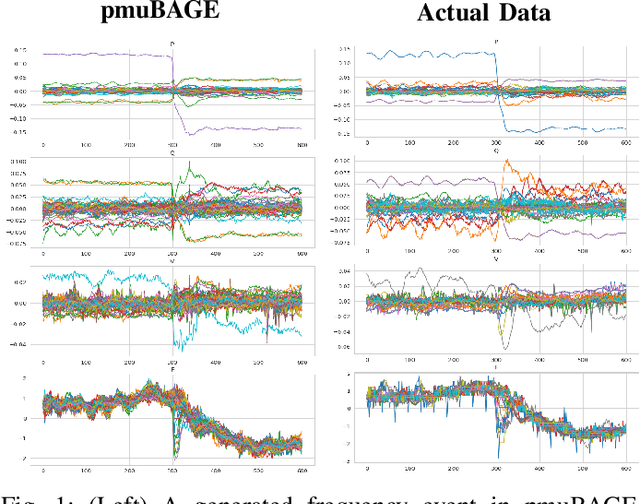
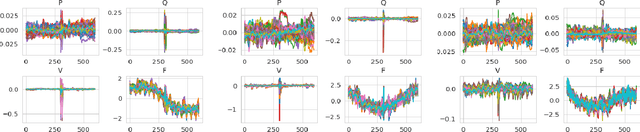
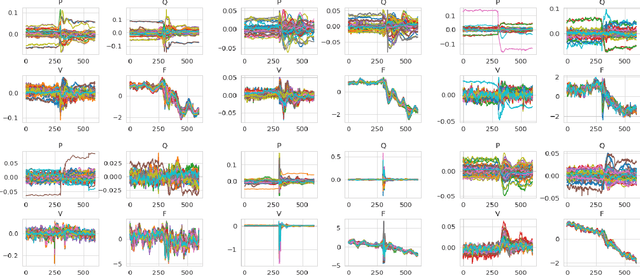
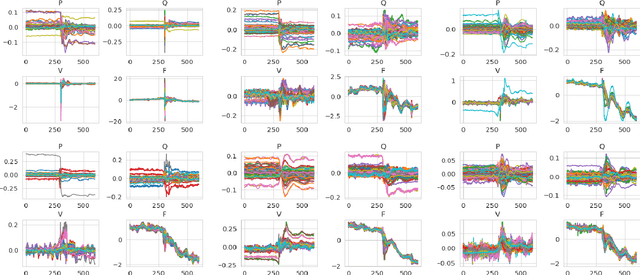
We present pmuGE (phasor measurement unit Generator of Events), one of the first data-driven generative model for power system event data. We have trained this model on thousands of actual events and created a dataset denoted pmuBAGE (the Benchmarking Assortment of Generated PMU Events). The dataset consists of almost 1000 instances of labeled event data to encourage benchmark evaluations on phasor measurement unit (PMU) data analytics. The dataset is available online for use by any researcher or practitioner in the field. PMU data are challenging to obtain, especially those covering event periods. Nevertheless, power system problems have recently seen phenomenal advancements via data-driven machine learning solutions - solutions created by researchers who were fortunate enough to obtain such PMU data. A highly accessible standard benchmarking dataset would enable a drastic acceleration of the development of successful machine learning techniques in this field. We propose a novel learning method based on the Event Participation Decomposition of Power System Events, which makes it possible to learn a generative model of PMU data during system anomalies. The model can create highly realistic event data without compromising the differential privacy of the PMUs used to train it. The dataset is available online for any researcher to use at the pmuBAGE Github Repository - https://github.com/NanpengYu/pmuBAGE. Part I - This is part I of a two part paper. In part I, we describe a high level overview of pmuBAGE, its creation, and the experiments used to test it. Part II will discuss the exact models used in its generation in far more detail.

Power System Event Identification based on Deep Neural Network with Information Loading

Online power system event identification and classification is crucial to enhancing the reliability of transmission systems. In this paper, we develop a deep neural network (DNN) based approach to identify and classify power system events by leveraging real-world measurements from hundreds of phasor measurement units (PMUs) and labels from thousands of events. Two innovative designs are embedded into the baseline model built on convolutional neural networks (CNNs) to improve the event classification accuracy. First, we propose a graph signal processing based PMU sorting algorithm to improve the learning efficiency of CNNs. Second, we deploy information loading based regularization to strike the right balance between memorization and generalization for the DNN. Numerical studies results based on real-world dataset from the Eastern Interconnection of the U.S power transmission grid show that the combination of PMU based sorting and the information loading based regularization techniques help the proposed DNN approach achieve highly accurate event identification and classification results.

On the Maximum Mutual Information Capacity of Neural Architectures

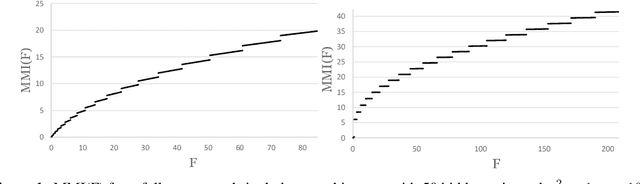
We derive the closed-form expression of the maximum mutual information - the maximum value of $I(X;Z)$ obtainable via training - for a broad family of neural network architectures. The quantity is essential to several branches of machine learning theory and practice. Quantitatively, we show that the maximum mutual information for these families all stem from generalizations of a single catch-all formula. Qualitatively, we show that the maximum mutual information of an architecture is most strongly influenced by the width of the smallest layer of the network - the "information bottleneck" in a different sense of the phrase, and by any statistical invariances captured by the architecture.

Improving Supervised Phase Identification Through the Theory of Information Losses

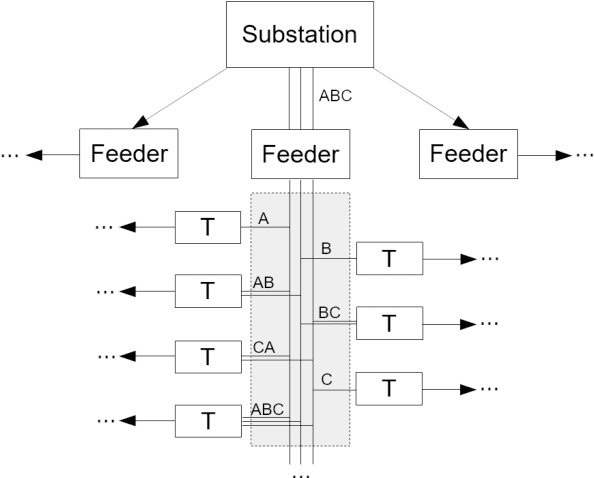
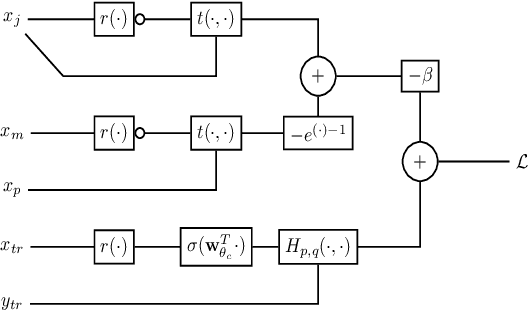
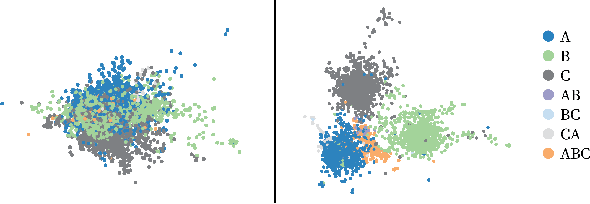
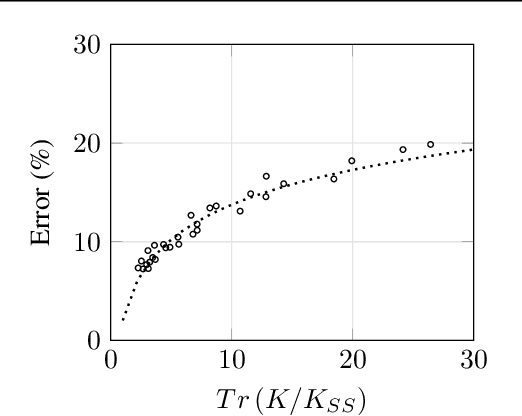
This paper considers the problem of Phase Identification in power distribution systems. In particular, it focuses on improving supervised learning accuracies by focusing on exploiting some of the problem's information theoretic properties. This focus, along with recent advances in Information Theoretic Machine Learning (ITML), helps us to create two new techniques. The first transforms a bound on information losses into a data selection technique. This is important because phase identification data labels are difficult to obtain in practice. The second interprets the properties of distribution systems in the terms of ITML. This allows us to obtain an improvement in the representation learned by any classifier applied to the problem. We tested these two techniques experimentally on real datasets and have found that they yield phenomenal performance in every case. In the most extreme case, they improve phase identification accuracy from $51.7\%$ to $97.3\%$. Furthermore, since many problems share the physical properties of phase identification exploited in this paper, the techniques can be applied to a wide range of similar problems.

Interpreting Active Learning Methods Through Information Losses

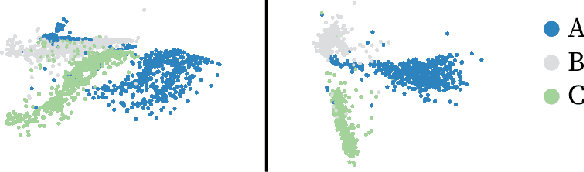
We propose a new way of interpreting active learning methods by analyzing the information `lost' upon sampling a random variable. We use some recent analytical developments of these losses to formally prove that facility location methods reduce these losses under mild assumptions, and to derive a new data dependent bound on information losses that can be used to evaluate other active learning methods. We show that this new bound is extremely tight to experiment, and further show that the bound has a decent predictive power for classification accuracy.

Asymptotic Finite Sample Information Losses in Neural Classifiers

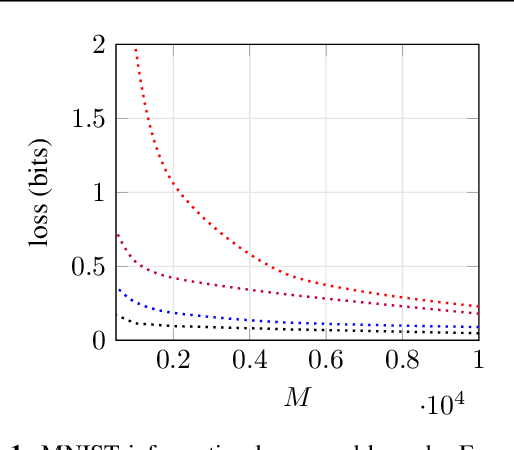
This paper considers the subject of information losses arising from finite datasets used in the training of neural classifiers. It proves a relationship between such losses and the product of the expected total variation of the estimated neural model with the information about the feature space contained in the hidden representation of that model. It then shows that this total variation drops extremely quickly with sample size. It ultimately obtains bounds on information losses that are less sensitive to input compression and much tighter than existing bounds. This brings about a tighter relevance of information theory to the training of neural networks, so a review of techniques for information estimation and control is provided. The paper then explains some potential uses of these bounds in the field of active learning, and then uses them to explain some recent experimental findings of information compression in neural networks which cannot be explained by previous work. It then uses the bounds to justify an information regularization term in the training of neural networks for low entropy feature space problems. Finally, the paper shows that, not only are these bounds much tighter than existing ones, but that these bounds correspond with experiments as well.