Advancements and Trends in Ultra-High-Resolution Image Processing: An Overview

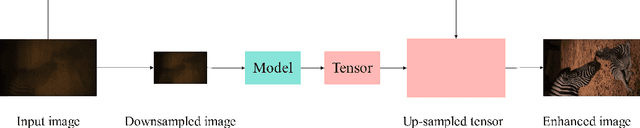
Currently, to further improve visual enjoyment, Ultra-High-Definition (UHD) images are catching wide attention. Here, UHD images are usually referred to as having a resolution greater than or equal to $3840 \times 2160$. However, since the imaging equipment is subject to environmental noise or equipment jitter, UHD images are prone to contrast degradation, blurring, low dynamic range, etc. To address these issues, a large number of algorithms for UHD image enhancement have been proposed. In this paper, we introduce the current state of UHD image enhancement from two perspectives, one is the application field and the other is the technology. In addition, we briefly explore its trends.

Single UHD Image Dehazing via Interpretable Pyramid Network

Currently, most single image dehazing models cannot run an ultra-high-resolution (UHD) image with a single GPU shader in real-time. To address the problem, we introduce the principle of infinite approximation of Taylor's theorem with the Laplace pyramid pattern to build a model which is capable of handling 4K hazy images in real-time. The N branch networks of the pyramid network correspond to the N constraint terms in Taylor's theorem. Low-order polynomials reconstruct the low-frequency information of the image (e.g. color, illumination). High-order polynomials regress the high-frequency information of the image (e.g. texture). In addition, we propose a Tucker reconstruction-based regularization term that acts on each branch network of the pyramid model. It further constrains the generation of anomalous signals in the feature space. Extensive experimental results demonstrate that our approach can not only run 4K images with haze in real-time on a single GPU (80FPS) but also has unparalleled interpretability. The developed method achieves state-of-the-art (SOTA) performance on two benchmarks (O/I-HAZE) and our updated 4KID dataset while providing the reliable groundwork for subsequent optimization schemes.