Blake Hunter
Unsupervised vehicle recognition using incremental reseeding of acoustic signatures
Feb 17, 2018
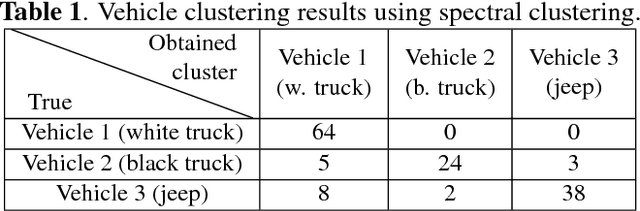
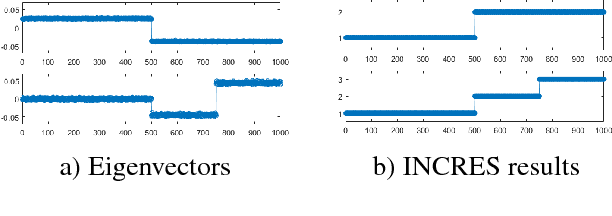
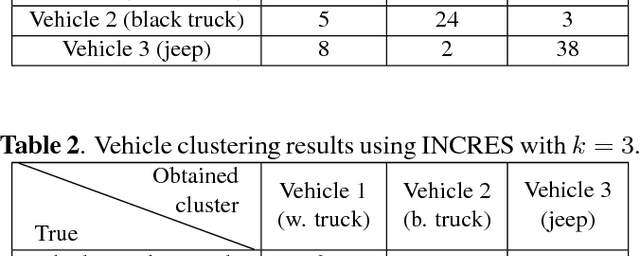
Abstract:Vehicle recognition and classification have broad applications, ranging from traffic flow management to military target identification. We demonstrate an unsupervised method for automated identification of moving vehicles from roadside audio sensors. Using a short-time Fourier transform to decompose audio signals, we treat the frequency signature in each time window as an individual data point. We then use a spectral embedding for dimensionality reduction. Based on the leading eigenvectors, we relate the performance of an incremental reseeding algorithm to that of spectral clustering. We find that incremental reseeding accurately identifies individual vehicles using their acoustic signatures.
Multislice Modularity Optimization in Community Detection and Image Segmentation
Nov 30, 2012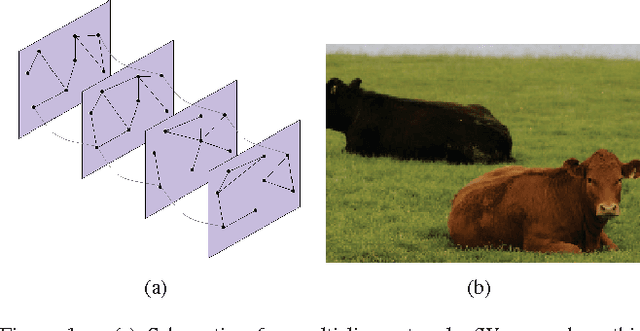
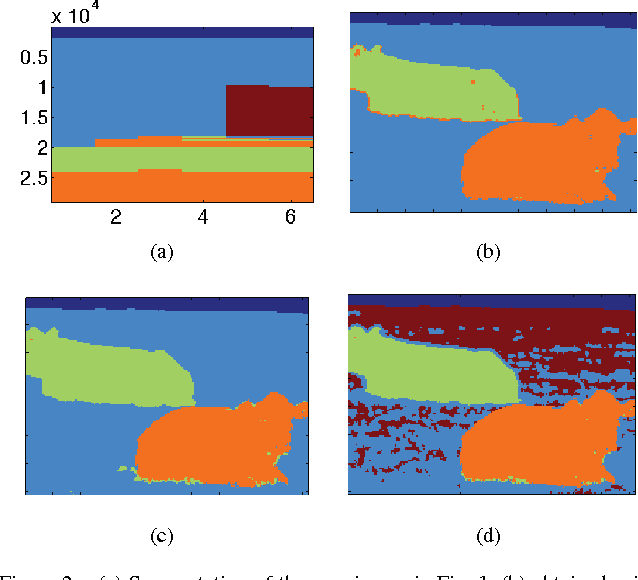
Abstract:Because networks can be used to represent many complex systems, they have attracted considerable attention in physics, computer science, sociology, and many other disciplines. One of the most important areas of network science is the algorithmic detection of cohesive groups (i.e., "communities") of nodes. In this paper, we algorithmically detect communities in social networks and image data by optimizing multislice modularity. A key advantage of modularity optimization is that it does not require prior knowledge of the number or sizes of communities, and it is capable of finding network partitions that are composed of communities of different sizes. By optimizing multislice modularity and subsequently calculating diagnostics on the resulting network partitions, it is thereby possible to obtain information about network structure across multiple system scales. We illustrate this method on data from both social networks and images, and we find that optimization of multislice modularity performs well on these two tasks without the need for extensive problem-specific adaptation. However, improving the computational speed of this method remains a challenging open problem.
Performance Analysis of Spectral Clustering on Compressed, Incomplete and Inaccurate Measurements
Nov 03, 2010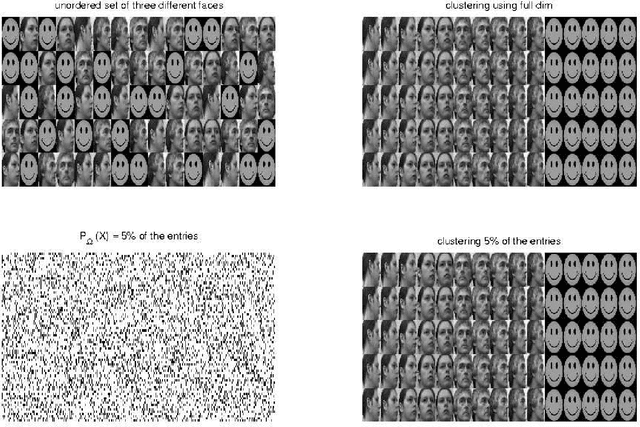
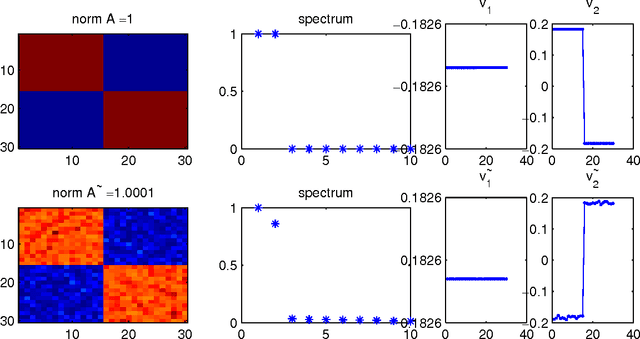
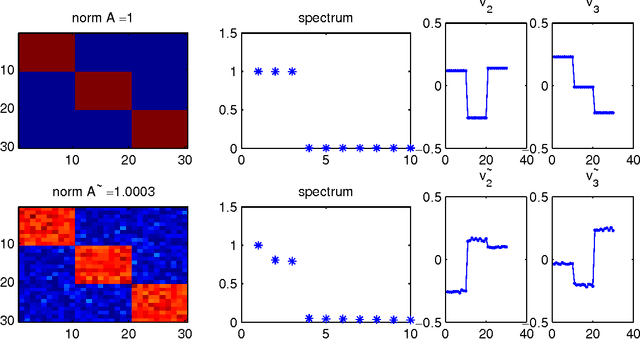
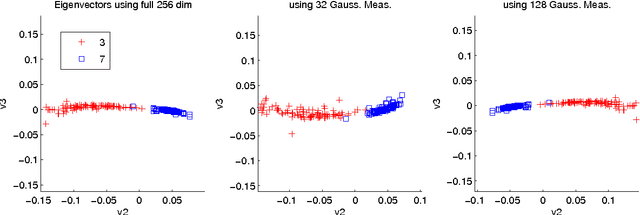
Abstract:Spectral clustering is one of the most widely used techniques for extracting the underlying global structure of a data set. Compressed sensing and matrix completion have emerged as prevailing methods for efficiently recovering sparse and partially observed signals respectively. We combine the distance preserving measurements of compressed sensing and matrix completion with the power of robust spectral clustering. Our analysis provides rigorous bounds on how small errors in the affinity matrix can affect the spectral coordinates and clusterability. This work generalizes the current perturbation results of two-class spectral clustering to incorporate multi-class clustering with k eigenvectors. We thoroughly track how small perturbation from using compressed sensing and matrix completion affect the affinity matrix and in succession the spectral coordinates. These perturbation results for multi-class clustering require an eigengap between the kth and (k+1)th eigenvalues of the affinity matrix, which naturally occurs in data with k well-defined clusters. Our theoretical guarantees are complemented with numerical results along with a number of examples of the unsupervised organization and clustering of image data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge