Learning by Grouping: A Multilevel Optimization Framework for Improving Fairness in Classification without Losing Accuracy

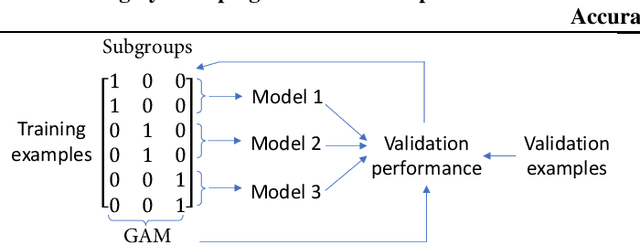
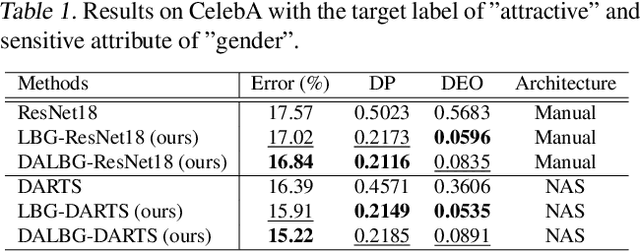
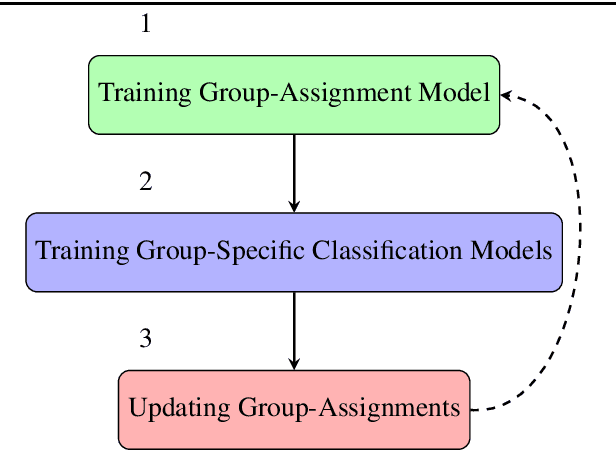
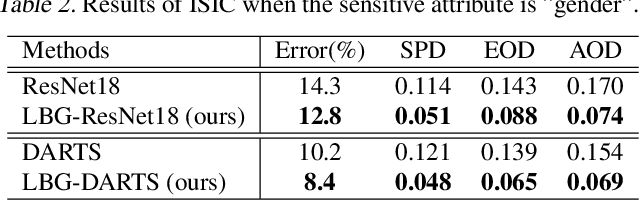
The integration of machine learning models in various real-world applications is becoming more prevalent to assist humans in their daily decision-making tasks as a result of recent advancements in this field. However, it has been discovered that there is a tradeoff between the accuracy and fairness of these decision-making tasks. In some cases, these AI systems can be unfair by exhibiting bias or discrimination against certain social groups, which can have severe consequences in real life. Inspired by one of the most well-known human learning skills called grouping, we address this issue by proposing a novel machine learning framework where the ML model learns to group a diverse set of problems into distinct subgroups to solve each subgroup using its specific sub-model. Our proposed framework involves three stages of learning, which are formulated as a three-level optimization problem: (i) learning to group problems into different subgroups; (ii) learning group-specific sub-models for problem-solving; and (iii) updating group assignments of training examples by minimizing the validation loss. These three learning stages are performed end-to-end in a joint manner using gradient descent. To improve fairness and accuracy, we develop an efficient optimization algorithm to solve this three-level optimization problem. To further reduce the risk of overfitting in small datasets, we incorporate domain adaptation techniques in the second stage of training. We further apply our method to neural architecture search. Extensive experiments on various datasets demonstrate our method's effectiveness and performance improvements in both fairness and accuracy. Our proposed Learning by Grouping can reduce overfitting and achieve state-of-the-art performances with fixed human-designed network architectures and searchable network architectures on various datasets.

Learning from Mistakes -- A Framework for Neural Architecture Search

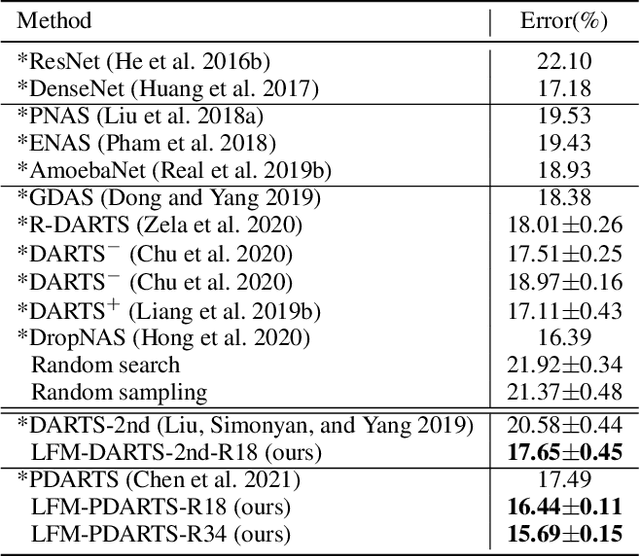
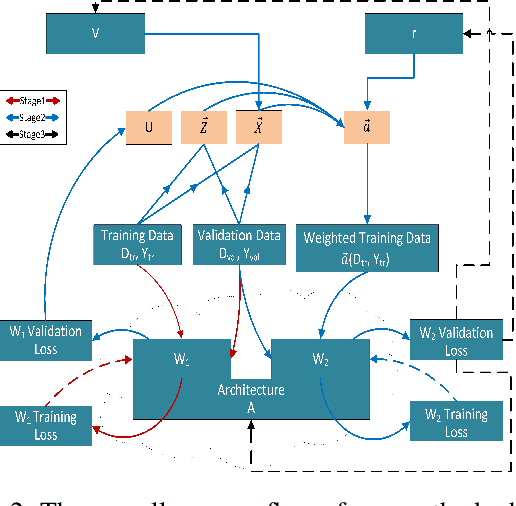
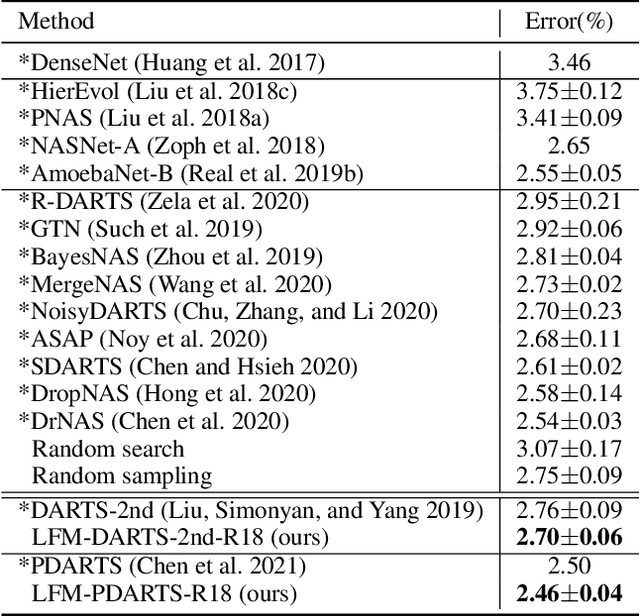
Learning from one's mistakes is an effective human learning technique where the learners focus more on the topics where mistakes were made, so as to deepen their understanding. In this paper, we investigate if this human learning strategy can be applied in machine learning. We propose a novel machine learning method called Learning From Mistakes (LFM), wherein the learner improves its ability to learn by focusing more on the mistakes during revision. We formulate LFM as a three-stage optimization problem: 1) learner learns; 2) learner re-learns focusing on the mistakes, and; 3) learner validates its learning. We develop an efficient algorithm to solve the LFM problem. We apply the LFM framework to neural architecture search on CIFAR-10, CIFAR-100, and Imagenet. Experimental results strongly demonstrate the effectiveness of our model.

Robust Deep Ordinal Regression Under Label Noise

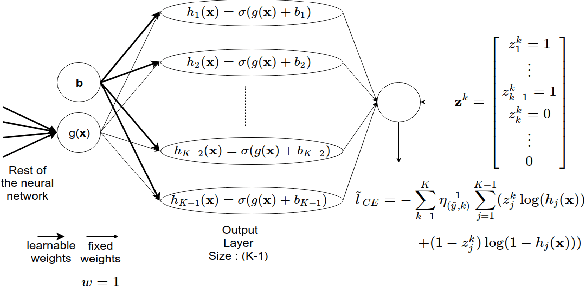
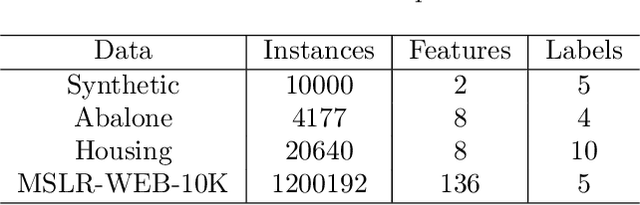
The real-world data is often susceptible to label noise, which might constrict the effectiveness of the existing state of the art algorithms for ordinal regression. Existing works on ordinal regression do not take label noise into account. We propose a theoretically grounded approach for class conditional label noise in ordinal regression problems. We present a deep learning implementation of two commonly used loss functions for ordinal regression that is both - 1) robust to label noise, and 2) rank consistent for a good ranking rule. We verify these properties of the algorithm empirically and show robustness to label noise on real data and rank consistency. To the best of our knowledge, this is the first approach for robust ordinal regression models.