Benoît Barbot
Université Paris-Est Créteil, France
Analyzing Robustness of Angluin's L* Algorithm in Presence of Noise
Sep 21, 2022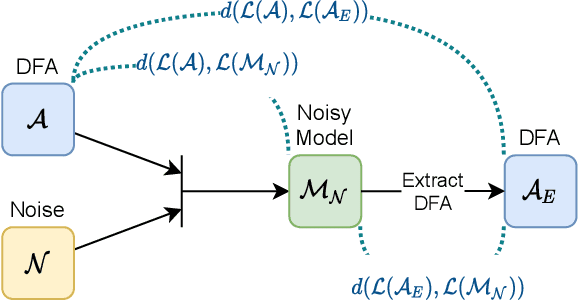
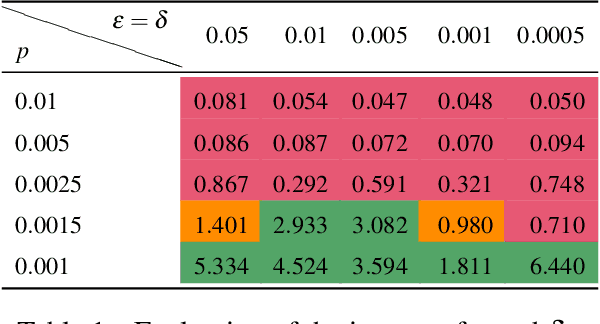
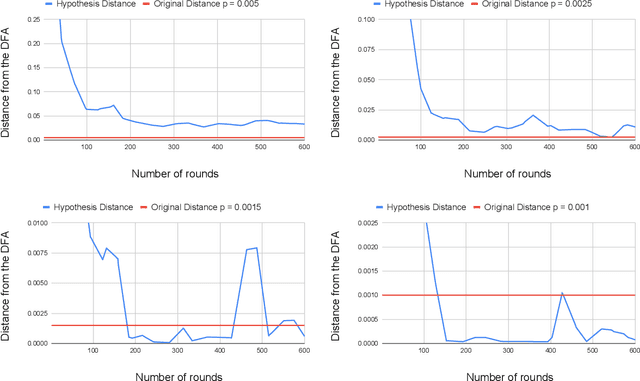
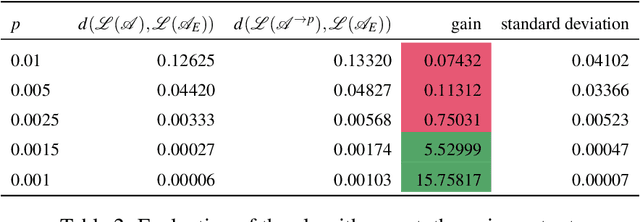
Abstract:Angluin's L* algorithm learns the minimal (complete) deterministic finite automaton (DFA) of a regular language using membership and equivalence queries. Its probabilistic approximatively correct (PAC) version substitutes an equivalence query by a large enough set of random membership queries to get a high level confidence to the answer. Thus it can be applied to any kind of (also non-regular) device and may be viewed as an algorithm for synthesizing an automaton abstracting the behavior of the device based on observations. Here we are interested on how Angluin's PAC learning algorithm behaves for devices which are obtained from a DFA by introducing some noise. More precisely we study whether Angluin's algorithm reduces the noise and produces a DFA closer to the original one than the noisy device. We propose several ways to introduce the noise: (1) the noisy device inverts the classification of words w.r.t. the DFA with a small probability, (2) the noisy device modifies with a small probability the letters of the word before asking its classification w.r.t. the DFA, and (3) the noisy device combines the classification of a word w.r.t. the DFA and its classification w.r.t. a counter automaton. Our experiments were performed on several hundred DFAs. Our main contributions, bluntly stated, consist in showing that: (1) Angluin's algorithm behaves well whenever the noisy device is produced by a random process, (2) but poorly with a structured noise, and, that (3) almost surely randomness yields systems with non-recursively enumerable languages.
* In Proceedings GandALF 2022, arXiv:2209.09333
Property-Directed Verification of Recurrent Neural Networks
Sep 22, 2020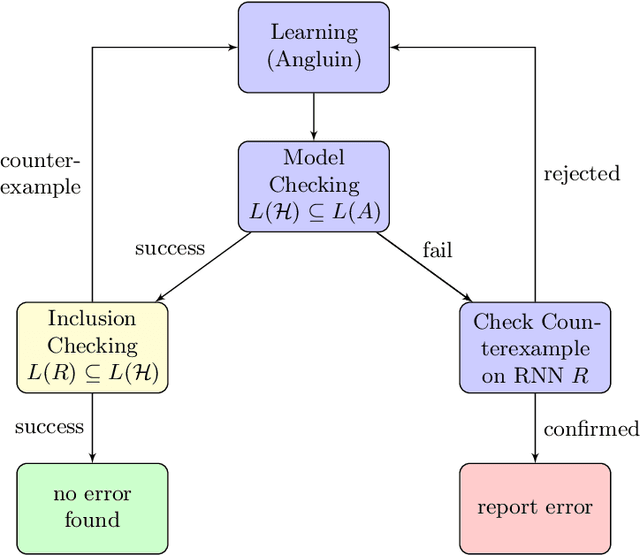
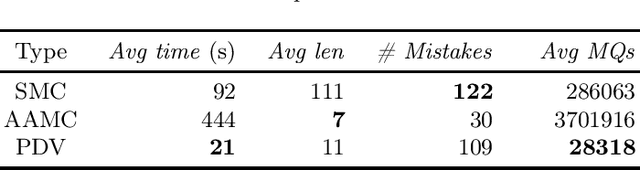

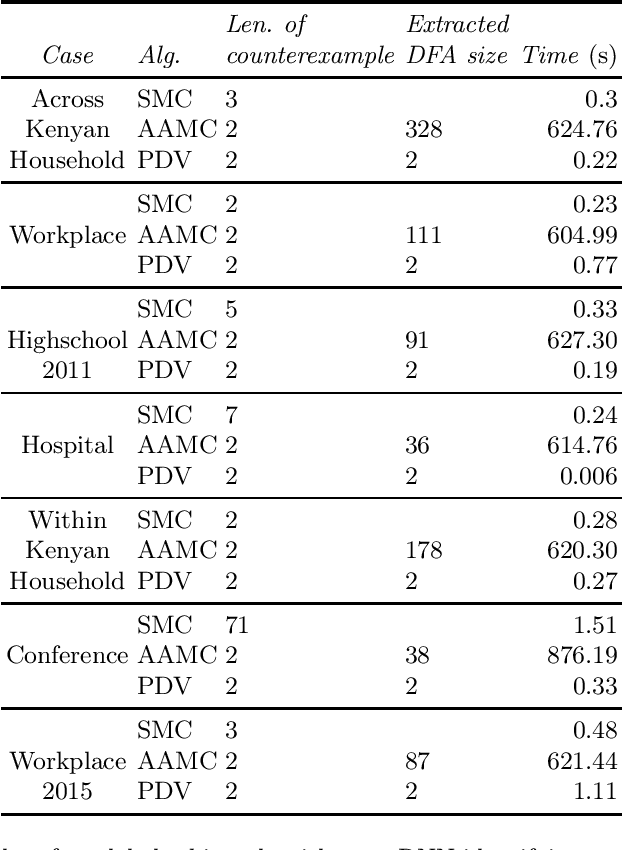
Abstract:This paper presents a property-directed approach to verifying recurrent neural networks (RNNs). To this end, we learn a deterministic finite automaton as a surrogate model from a given RNN using active automata learning. This model may then be analyzed using model checking as verification technique. The term property-directed reflects the idea that our procedure is guided and controlled by the given property rather than performing the two steps separately. We show that this not only allows us to discover small counterexamples fast, but also to generalize them by pumping towards faulty flows hinting at the underlying error in the RNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge