Benedict Brown
Efficient Spatially Adaptive Convolution and Correlation
Jun 23, 2020
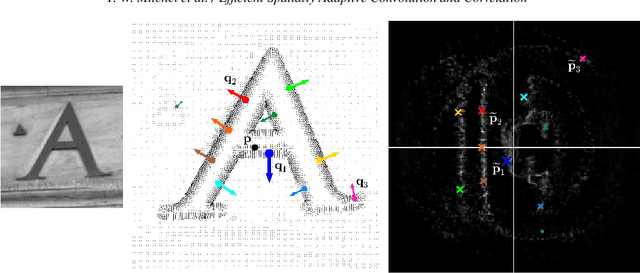

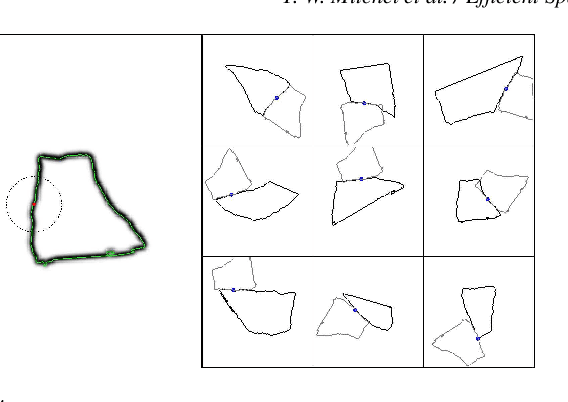
Abstract:Fast methods for convolution and correlation underlie a variety of applications in computer vision and graphics, including efficient filtering, analysis, and simulation. However, standard convolution and correlation are inherently limited to fixed filters: spatial adaptation is impossible without sacrificing efficient computation. In early work, Freeman and Adelson have shown how steerable filters can address this limitation, providing a way for rotating the filter as it is passed over the signal. In this work, we provide a general, representation-theoretic, framework that allows for spatially varying linear transformations to be applied to the filter. This framework allows for efficient implementation of extended convolution and correlation for transformation groups such as rotation (in 2D and 3D) and scale, and provides a new interpretation for previous methods including steerable filters and the generalized Hough transform. We present applications to pattern matching, image feature description, vector field visualization, and adaptive image filtering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge