Quantifying the Uncertainty in Model Parameters Using Gaussian Process-Based Markov Chain Monte Carlo: An Application to Cardiac Electrophysiological Models

Estimation of patient-specific model parameters is important for personalized modeling, although sparse and noisy clinical data can introduce significant uncertainty in the estimated parameter values. This importance source of uncertainty, if left unquantified, will lead to unknown variability in model outputs that hinder their reliable adoptions. Probabilistic estimation model parameters, however, remains an unresolved challenge because standard Markov Chain Monte Carlo sampling requires repeated model simulations that are computationally infeasible. A common solution is to replace the simulation model with a computationally-efficient surrogate for a faster sampling. However, by sampling from an approximation of the exact posterior probability density function (pdf) of the parameters, the efficiency is gained at the expense of sampling accuracy. In this paper, we address this issue by integrating surrogate modeling into Metropolis Hasting (MH) sampling of the exact posterior pdfs to improve its acceptance rate. It is done by first quickly constructing a Gaussian process (GP) surrogate of the exact posterior pdfs using deterministic optimization. This efficient surrogate is then used to modify commonly-used proposal distributions in MH sampling such that only proposals accepted by the surrogate will be tested by the exact posterior pdf for acceptance/rejection, reducing unnecessary model simulations at unlikely candidates. Synthetic and real-data experiments using the presented method show a significant gain in computational efficiency without compromising the accuracy. In addition, insights into the non-identifiability and heterogeneity of tissue properties can be gained from the obtained posterior distributions.

High-dimensional Bayesian Optimization of Personalized Cardiac Model Parameters via an Embedded Generative Model

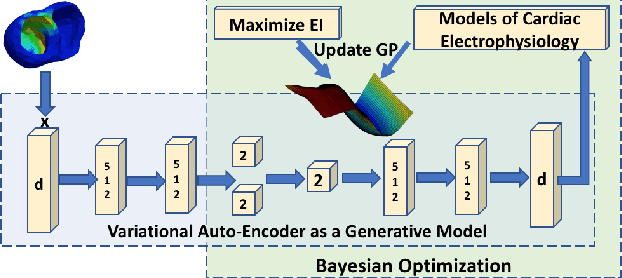
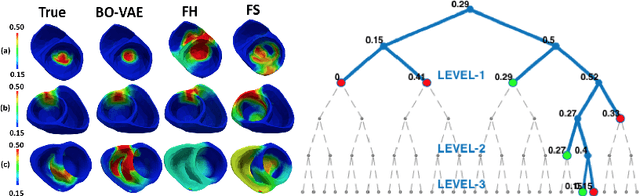
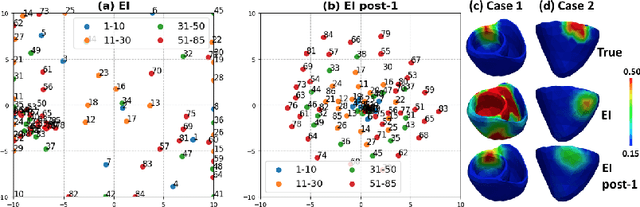
The estimation of patient-specific tissue properties in the form of model parameters is important for personalized physiological models. However, these tissue properties are spatially varying across the underlying anatomical model, presenting a significance challenge of high-dimensional (HD) optimization at the presence of limited measurement data. A common solution to reduce the dimension of the parameter space is to explicitly partition the anatomical mesh, either into a fixed small number of segments or a multi-scale hierarchy. This anatomy-based reduction of parameter space presents a fundamental bottleneck to parameter estimation, resulting in solutions that are either too low in resolution to reflect tissue heterogeneity, or too high in dimension to be reliably estimated within feasible computation. In this paper, we present a novel concept that embeds a generative variational auto-encoder (VAE) into the objective function of Bayesian optimization, providing an implicit low-dimensional (LD) search space that represents the generative code of the HD spatially-varying tissue properties. In addition, the VAE-encoded knowledge about the generative code is further used to guide the exploration of the search space. The presented method is applied to estimating tissue excitability in a cardiac electrophysiological model. Synthetic and real-data experiments demonstrate its ability to improve the accuracy of parameter estimation with more than 10x gain in efficiency.