Austin Egbert
Changepoint Detection for Real-Time Spectrum Sharing Radar
Jun 30, 2022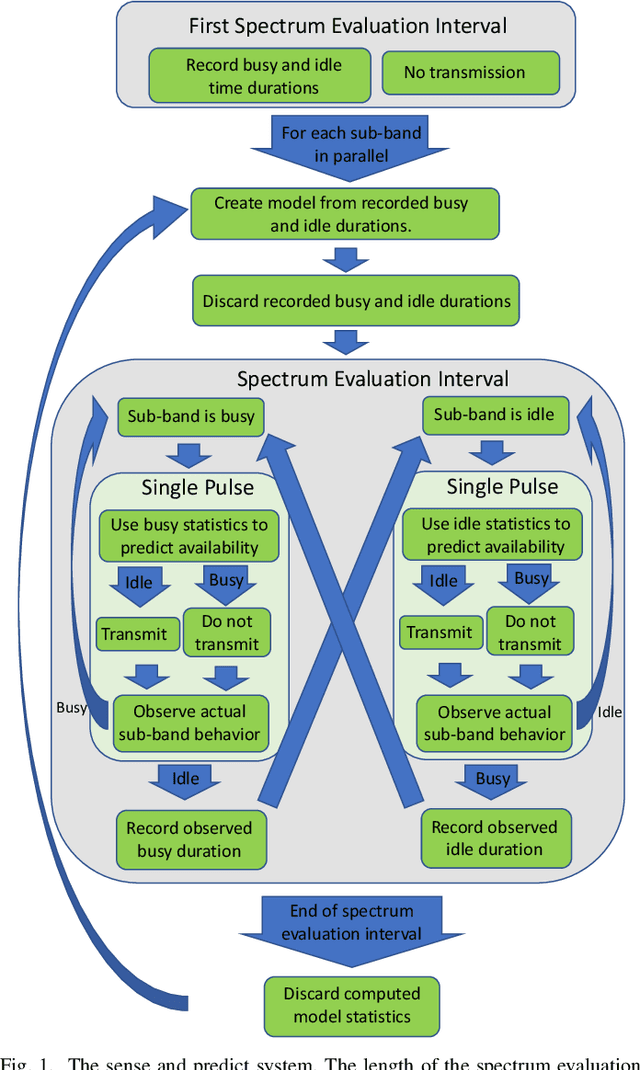
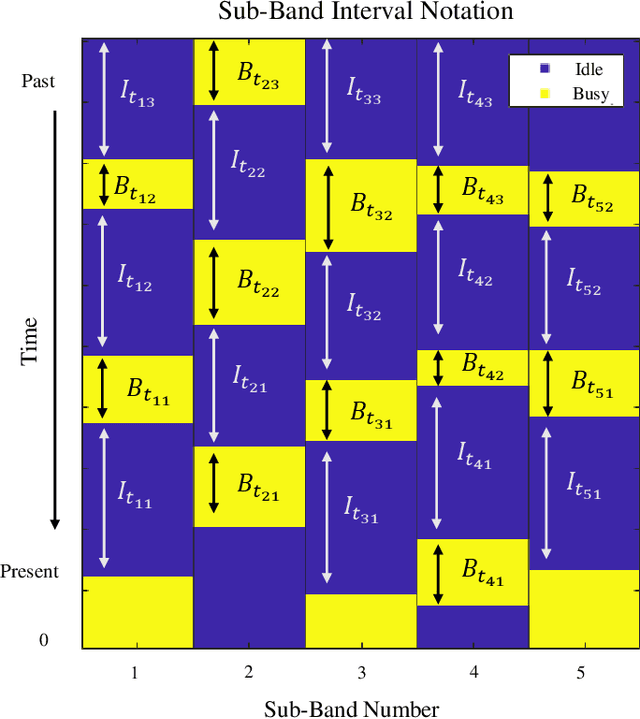
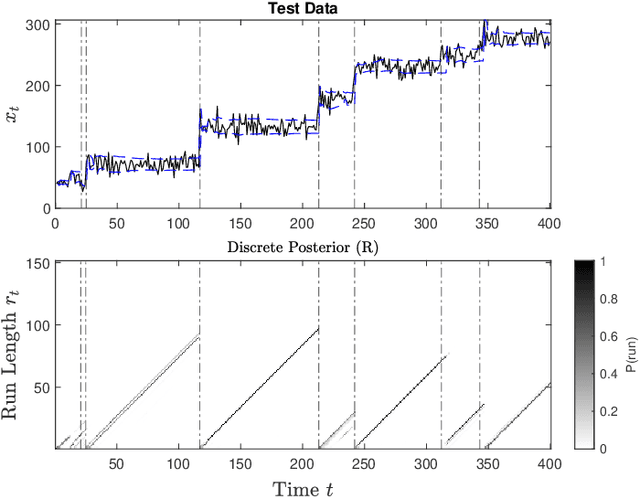
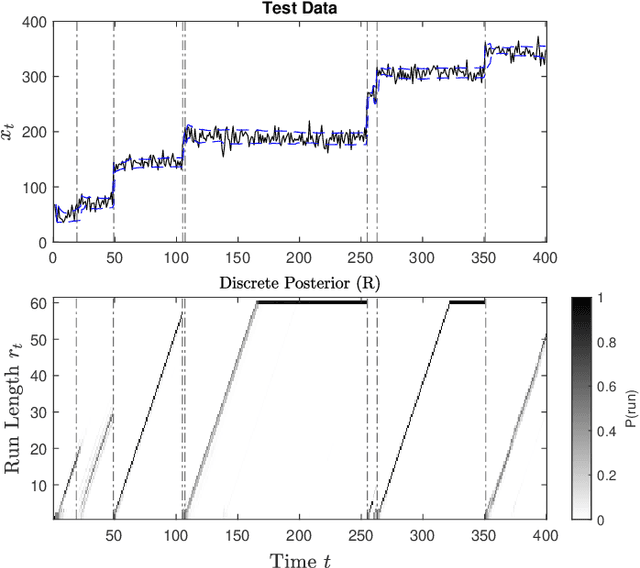
Abstract:Radar must adapt to changing environments, and we propose changepoint detection as a method to do so. In the world of increasingly congested radio frequencies, radars must adapt to avoid interference. Many radar systems employ the prediction action cycle to proactively determine transmission mode while spectrum sharing. This method constructs and implements a model of the environment to predict unused frequencies, and then transmits in this predicted availability. For these selection strategies, performance is directly reliant on the quality of the underlying environmental models. In order to keep up with a changing environment, these models can employ changepoint detection. Changepoint detection is the identification of sudden changes, or changepoints, in the distribution from which data is drawn. This information allows the models to discard "garbage" data from a previous distribution, which has no relation to the current state of the environment. In this work, bayesian online changepoint detection (BOCD) is applied to the sense and predict algorithm to increase the accuracy of its models and improve its performance. In the context of spectrum sharing, these changepoints represent interferers leaving and entering the spectral environment. The addition of changepoint detection allows for dynamic and robust spectrum sharing even as interference patterns change dramatically. BOCD is especially advantageous because it enables online changepoint detection, allowing models to be updated continuously as data are collected. This strategy can also be applied to many other predictive algorithms that create models in a changing environment.
Dilated POCS: Minimax Convex Optimization
Jun 09, 2022
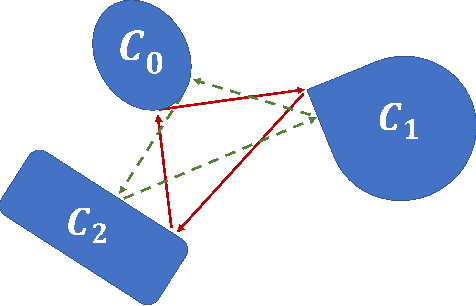

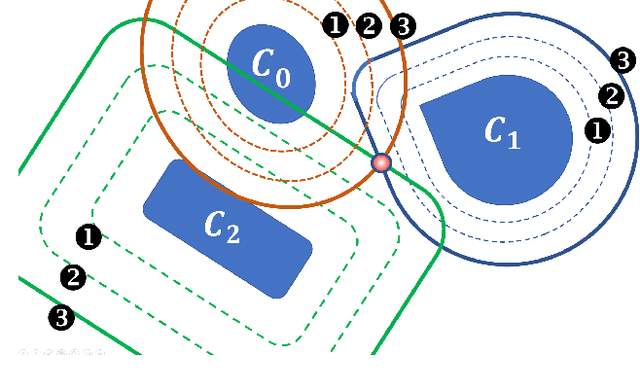
Abstract:Alternating projection onto convex sets (POCS) provides an iterative procedure to find a signal that satisfies two or more convex constraints when the sets intersect. For nonintersecting constraints, the method of simultaneous projections produces a minimum mean square error (MSE) solution. In certain cases, a minimax solution is more desirable. Generating a minimax solution is possible using dilated POCS (D-POCS). The minimax solution uses morphological dilation of nonintersecting signal convex constraints. The sets are progressively dilated to the point where there is intersection at a minimax solution. Examples are given contrasting the MSE and minimax solutions in problem of tomographic reconstruction of images. Lastly, morphological erosion of signal sets is suggested as a method to shrink the overlap when sets intersect at more than one point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge