Dilated POCS: Minimax Convex Optimization

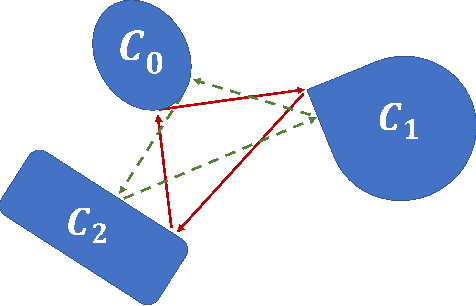
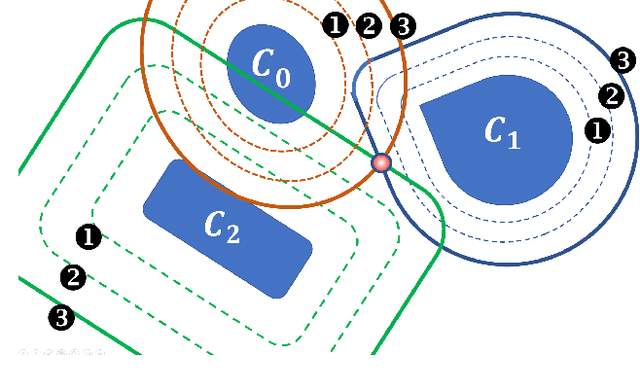
Alternating projection onto convex sets (POCS) provides an iterative procedure to find a signal that satisfies two or more convex constraints when the sets intersect. For nonintersecting constraints, the method of simultaneous projections produces a minimum mean square error (MSE) solution. In certain cases, a minimax solution is more desirable. Generating a minimax solution is possible using dilated POCS (D-POCS). The minimax solution uses morphological dilation of nonintersecting signal convex constraints. The sets are progressively dilated to the point where there is intersection at a minimax solution. Examples are given contrasting the MSE and minimax solutions in problem of tomographic reconstruction of images. Lastly, morphological erosion of signal sets is suggested as a method to shrink the overlap when sets intersect at more than one point.