Dilated POCS: Minimax Convex Optimization
Paper and Code
Jun 09, 2022
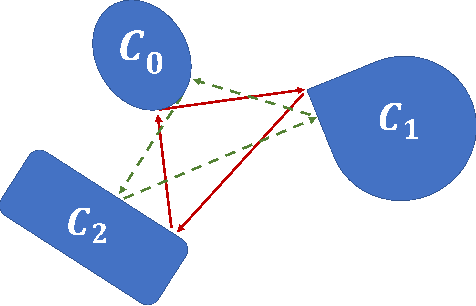

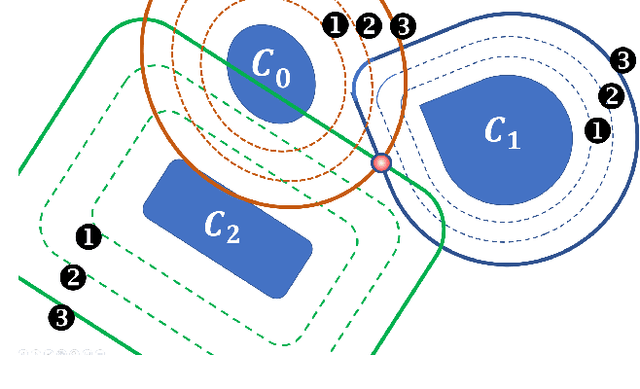
Alternating projection onto convex sets (POCS) provides an iterative procedure to find a signal that satisfies two or more convex constraints when the sets intersect. For nonintersecting constraints, the method of simultaneous projections produces a minimum mean square error (MSE) solution. In certain cases, a minimax solution is more desirable. Generating a minimax solution is possible using dilated POCS (D-POCS). The minimax solution uses morphological dilation of nonintersecting signal convex constraints. The sets are progressively dilated to the point where there is intersection at a minimax solution. Examples are given contrasting the MSE and minimax solutions in problem of tomographic reconstruction of images. Lastly, morphological erosion of signal sets is suggested as a method to shrink the overlap when sets intersect at more than one point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge