Audrūnas Gruslys
The Advantage Regret-Matching Actor-Critic
Aug 27, 2020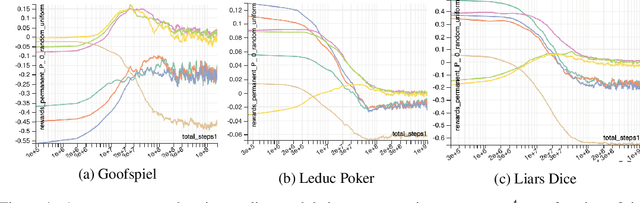
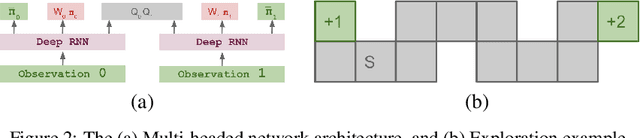

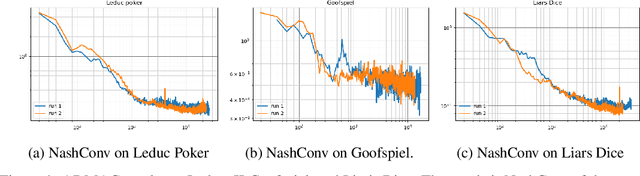
Abstract:Regret minimization has played a key role in online learning, equilibrium computation in games, and reinforcement learning (RL). In this paper, we describe a general model-free RL method for no-regret learning based on repeated reconsideration of past behavior. We propose a model-free RL algorithm, the AdvantageRegret-Matching Actor-Critic (ARMAC): rather than saving past state-action data, ARMAC saves a buffer of past policies, replaying through them to reconstruct hindsight assessments of past behavior. These retrospective value estimates are used to predict conditional advantages which, combined with regret matching, produces a new policy. In particular, ARMAC learns from sampled trajectories in a centralized training setting, without requiring the application of importance sampling commonly used in Monte Carlo counterfactual regret (CFR) minimization; hence, it does not suffer from excessive variance in large environments. In the single-agent setting, ARMAC shows an interesting form of exploration by keeping past policies intact. In the multiagent setting, ARMAC in self-play approaches Nash equilibria on some partially-observable zero-sum benchmarks. We provide exploitability estimates in the significantly larger game of betting-abstracted no-limit Texas Hold'em.
Memory-Efficient Backpropagation Through Time
Jun 10, 2016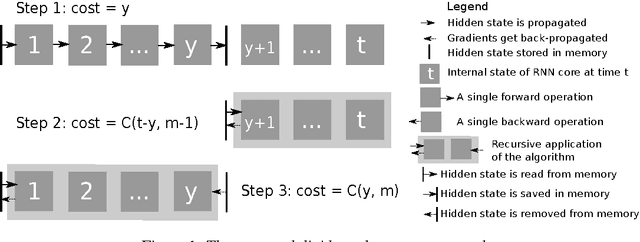
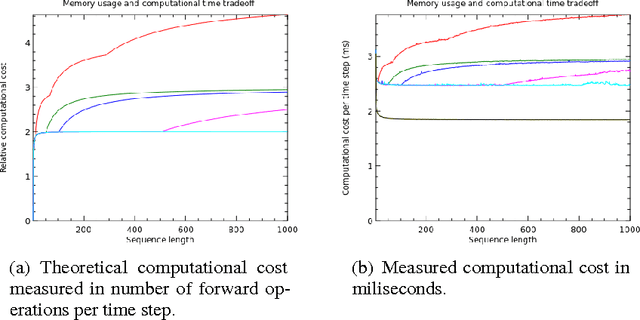
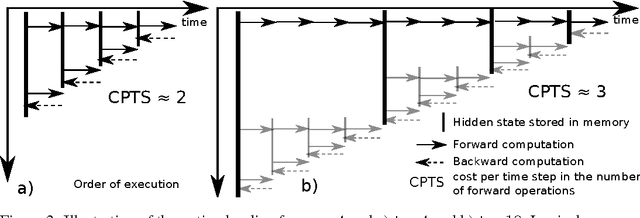
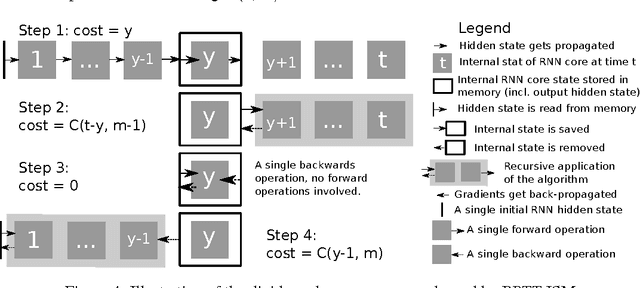
Abstract:We propose a novel approach to reduce memory consumption of the backpropagation through time (BPTT) algorithm when training recurrent neural networks (RNNs). Our approach uses dynamic programming to balance a trade-off between caching of intermediate results and recomputation. The algorithm is capable of tightly fitting within almost any user-set memory budget while finding an optimal execution policy minimizing the computational cost. Computational devices have limited memory capacity and maximizing a computational performance given a fixed memory budget is a practical use-case. We provide asymptotic computational upper bounds for various regimes. The algorithm is particularly effective for long sequences. For sequences of length 1000, our algorithm saves 95\% of memory usage while using only one third more time per iteration than the standard BPTT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge