Generalized Sparse Additive Models

We present a unified framework for estimation and analysis of generalized additive models in high dimensions. The framework defines a large class of penalized regression estimators, encompassing many existing methods. An efficient computational algorithm for this class is presented that easily scales to thousands of observations and features. We prove minimax optimal convergence bounds for this class under a weak compatibility condition. In addition, we characterize the rate of convergence when this compatibility condition is not met. Finally, we also show that the optimal penalty parameters for structure and sparsity penalties in our framework are linked, allowing cross-validation to be conducted over only a single tuning parameter. We complement our theoretical results with empirical studies comparing some existing methods within this framework.

Wavelet regression and additive models for irregularly spaced data

We present a novel approach for nonparametric regression using wavelet basis functions. Our proposal, $\texttt{waveMesh}$, can be applied to non-equispaced data with sample size not necessarily a power of 2. We develop an efficient proximal gradient descent algorithm for computing the estimator and establish adaptive minimax convergence rates. The main appeal of our approach is that it naturally extends to additive and sparse additive models for a potentially large number of covariates. We prove minimax optimal convergence rates under a weak compatibility condition for sparse additive models. The compatibility condition holds when we have a small number of covariates. Additionally, we establish convergence rates for when the condition is not met. We complement our theoretical results with empirical studies comparing $\texttt{waveMesh}$ to existing methods.

Nonparametric Regression with Adaptive Truncation via a Convex Hierarchical Penalty

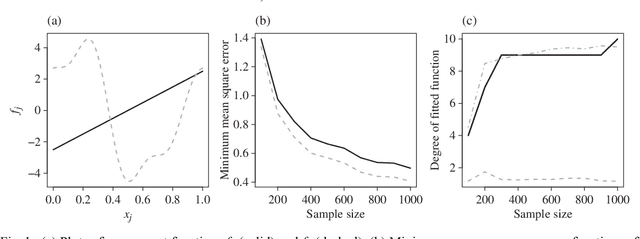
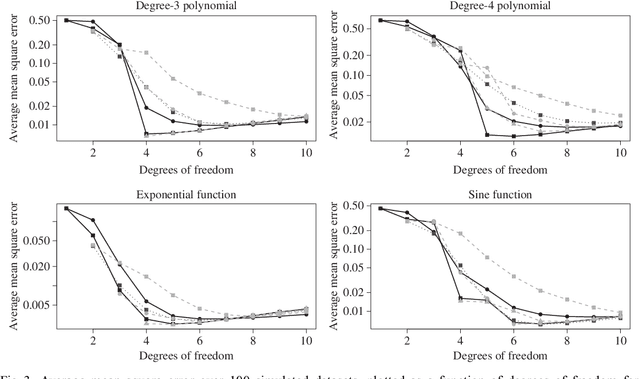
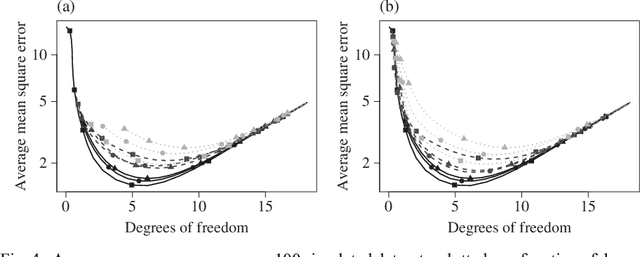
We consider the problem of non-parametric regression with a potentially large number of covariates. We propose a convex, penalized estimation framework that is particularly well-suited for high-dimensional sparse additive models. The proposed approach combines appealing features of finite basis representation and smoothing penalties for non-parametric estimation. In particular, in the case of additive models, a finite basis representation provides a parsimonious representation for fitted functions but is not adaptive when component functions posses different levels of complexity. On the other hand, a smoothing spline type penalty on the component functions is adaptive but does not offer a parsimonious representation of the estimated function. The proposed approach simultaneously achieves parsimony and adaptivity in a computationally efficient framework. We demonstrate these properties through empirical studies on both real and simulated datasets. We show that our estimator converges at the minimax rate for functions within a hierarchical class. We further establish minimax rates for a large class of sparse additive models. The proposed method is implemented using an efficient algorithm that scales similarly to the Lasso with the number of covariates and samples size.

Convex Modeling of Interactions with Strong Heredity

We consider the task of fitting a regression model involving interactions among a potentially large set of covariates, in which we wish to enforce strong heredity. We propose FAMILY, a very general framework for this task. Our proposal is a generalization of several existing methods, such as VANISH [Radchenko and James, 2010], hierNet [Bien et al., 2013], the all-pairs lasso, and the lasso using only main effects. It can be formulated as the solution to a convex optimization problem, which we solve using an efficient alternating directions method of multipliers (ADMM) algorithm. This algorithm has guaranteed convergence to the global optimum, can be easily specialized to any convex penalty function of interest, and allows for a straightforward extension to the setting of generalized linear models. We derive an unbiased estimator of the degrees of freedom of FAMILY, and explore its performance in a simulation study and on an HIV sequence data set.