Nonparametric Regression with Adaptive Truncation via a Convex Hierarchical Penalty
Paper and Code
Dec 01, 2016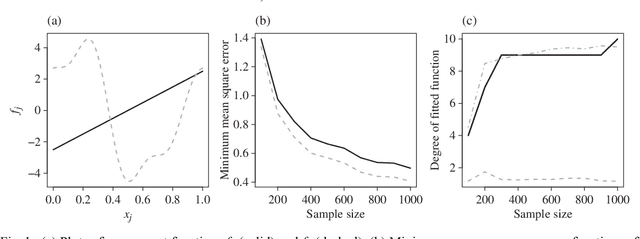
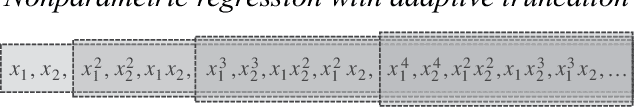
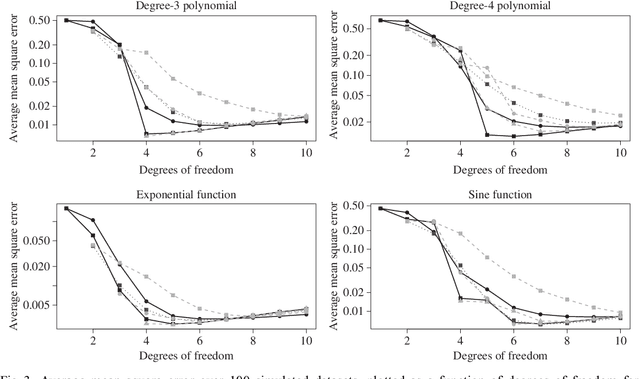
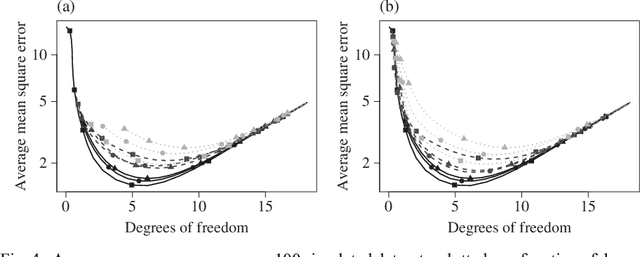
We consider the problem of non-parametric regression with a potentially large number of covariates. We propose a convex, penalized estimation framework that is particularly well-suited for high-dimensional sparse additive models. The proposed approach combines appealing features of finite basis representation and smoothing penalties for non-parametric estimation. In particular, in the case of additive models, a finite basis representation provides a parsimonious representation for fitted functions but is not adaptive when component functions posses different levels of complexity. On the other hand, a smoothing spline type penalty on the component functions is adaptive but does not offer a parsimonious representation of the estimated function. The proposed approach simultaneously achieves parsimony and adaptivity in a computationally efficient framework. We demonstrate these properties through empirical studies on both real and simulated datasets. We show that our estimator converges at the minimax rate for functions within a hierarchical class. We further establish minimax rates for a large class of sparse additive models. The proposed method is implemented using an efficient algorithm that scales similarly to the Lasso with the number of covariates and samples size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge