No-Regret Algorithms for Safe Bayesian Optimization with Monotonicity Constraints

We consider the problem of sequentially maximizing an unknown function $f$ over a set of actions of the form $(s,\mathbf{x})$, where the selected actions must satisfy a safety constraint with respect to an unknown safety function $g$. We model $f$ and $g$ as lying in a reproducing kernel Hilbert space (RKHS), which facilitates the use of Gaussian process methods. While existing works for this setting have provided algorithms that are guaranteed to identify a near-optimal safe action, the problem of attaining low cumulative regret has remained largely unexplored, with a key challenge being that expanding the safe region can incur high regret. To address this challenge, we show that if $g$ is monotone with respect to just the single variable $s$ (with no such constraint on $f$), sublinear regret becomes achievable with our proposed algorithm. In addition, we show that a modified version of our algorithm is able to attain sublinear regret (for suitably defined notions of regret) for the task of finding a near-optimal $s$ corresponding to every $\mathbf{x}$, as opposed to only finding the global safe optimum. Our findings are supported with empirical evaluations on various objective and safety functions.

Benefits of Monotonicity in Safe Exploration with Gaussian Processes

We consider the problem of sequentially maximising an unknown function over a set of actions while ensuring that every sampled point has a function value below a given safety threshold. We model the function using kernel-based and Gaussian process methods, while differing from previous works in our assumption that the function is monotonically increasing with respect to a safety variable. This assumption is motivated by various practical applications such as adaptive clinical trial design and robotics. Taking inspiration from the GP-UCB and SafeOpt algorithms, we propose an algorithm, monotone safe UCB (M-SafeUCB) for this task. We show that M-SafeUCB enjoys theoretical guarantees in terms of safety, a suitably-defined regret notion, and approximately finding the entire safe boundary. In addition, we illustrate that the monotonicity assumption yields significant benefits in terms of both the guarantees obtained and the algorithmic simplicity. We support our theoretical findings by performing empirical evaluations on a variety of functions.

Stochastic Linear Bandits Robust to Adversarial Attacks

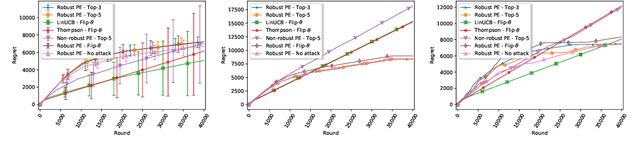
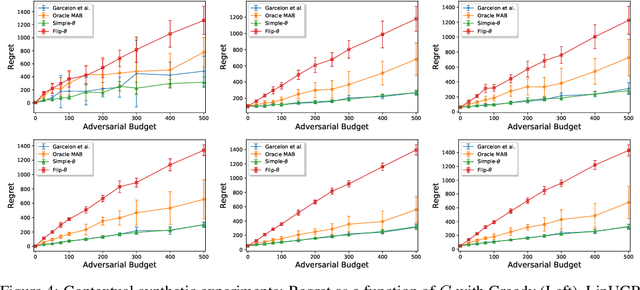
We consider a stochastic linear bandit problem in which the rewards are not only subject to random noise, but also adversarial attacks subject to a suitable budget $C$ (i.e., an upper bound on the sum of corruption magnitudes across the time horizon). We provide two variants of a Robust Phased Elimination algorithm, one that knows $C$ and one that does not. Both variants are shown to attain near-optimal regret in the non-corrupted case $C = 0$, while incurring additional additive terms respectively having a linear and quadratic dependency on $C$ in general. We present algorithm independent lower bounds showing that these additive terms are near-optimal. In addition, in a contextual setting, we revisit a setup of diverse contexts, and show that a simple greedy algorithm is provably robust with a near-optimal additive regret term, despite performing no explicit exploration and not knowing $C$.

Resisting Adversarial Attacks using Gaussian Mixture Variational Autoencoders

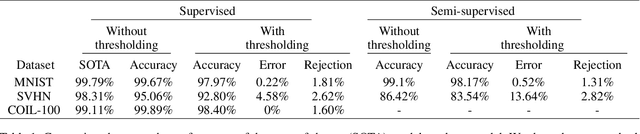
Susceptibility of deep neural networks to adversarial attacks poses a major theoretical and practical challenge. All efforts to harden classifiers against such attacks have seen limited success. Two distinct categories of samples to which deep networks are vulnerable, "adversarial samples" and "fooling samples", have been tackled separately so far due to the difficulty posed when considered together. In this work, we show how one can address them both under one unified framework. We tie a discriminative model with a generative model, rendering the adversarial objective to entail a conflict. Our model has the form of a variational autoencoder, with a Gaussian mixture prior on the latent vector. Each mixture component of the prior distribution corresponds to one of the classes in the data. This enables us to perform selective classification, leading to the rejection of adversarial samples instead of misclassification. Our method inherently provides a way of learning a selective classifier in a semi-supervised scenario as well, which can resist adversarial attacks. We also show how one can reclassify the rejected adversarial samples.