Arjun Rajkumar
Comfetch: Federated Learning of Large Networks on Memory-Constrained Clients via Sketching
Sep 17, 2021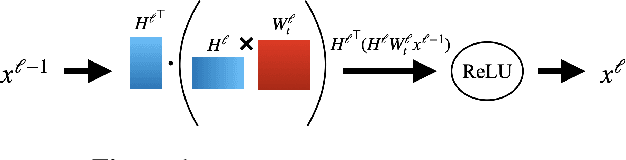
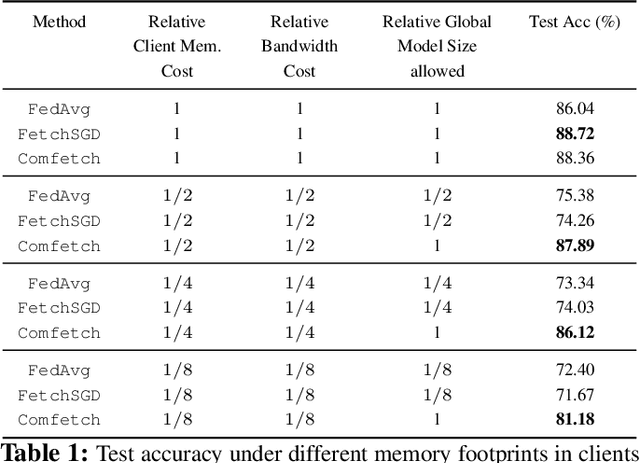
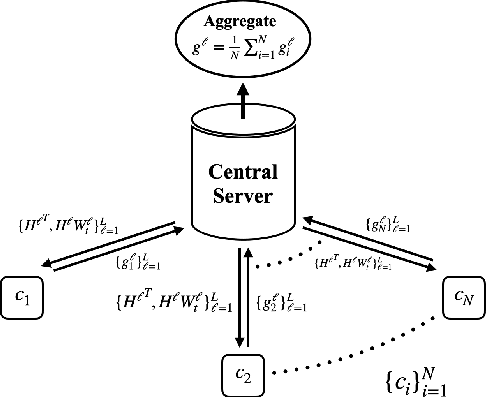
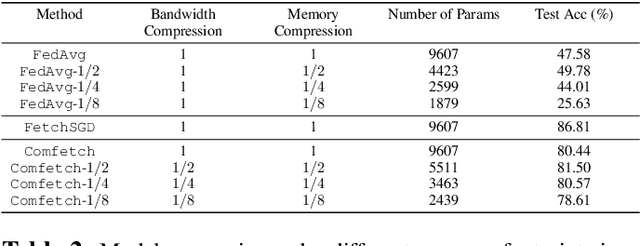
Abstract:A popular application of federated learning is using many clients to train a deep neural network, the parameters of which are maintained on a central server. While recent efforts have focused on reducing communication complexity, existing algorithms assume that each participating client is able to download the current and full set of parameters, which may not be a practical assumption depending on the memory constraints of clients such as mobile devices. In this work, we propose a novel algorithm Comfetch, which allows clients to train large networks using compressed versions of the global architecture via Count Sketch, thereby reducing communication and local memory costs. We provide a theoretical convergence guarantee and experimentally demonstrate that it is possible to learn large networks, such as a deep convolutional network and an LSTM, through federated agents training on their sketched counterparts. The resulting global models exhibit competitive test accuracy when compared against the state-of-the-art FetchSGD and the classical FedAvg, both of which require clients to download the full architecture.
Practical and Fast Momentum-Based Power Methods
Aug 20, 2021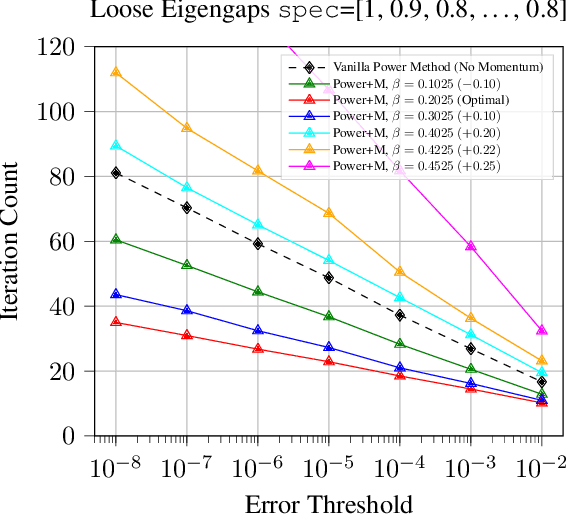
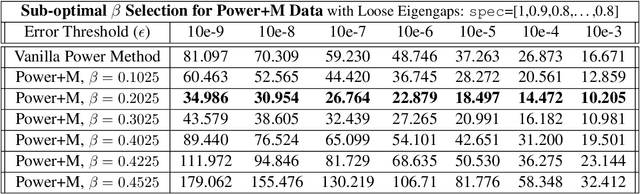
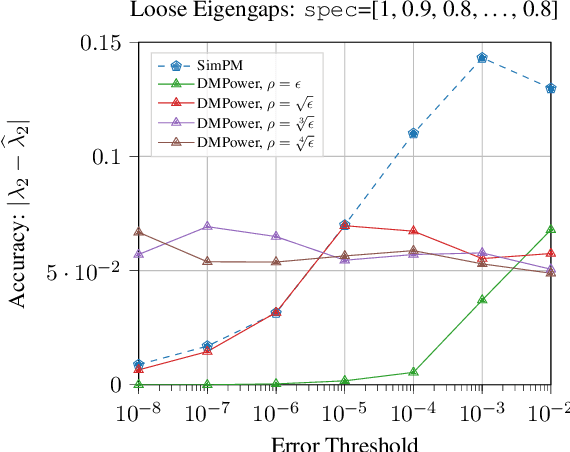
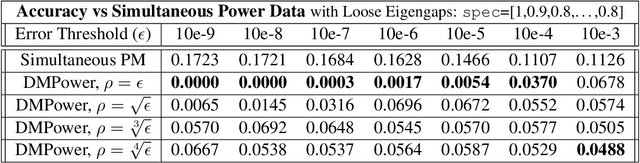
Abstract:The power method is a classical algorithm with broad applications in machine learning tasks, including streaming PCA, spectral clustering, and low-rank matrix approximation. The distilled purpose of the vanilla power method is to determine the largest eigenvalue (in absolute modulus) and its eigenvector of a matrix. A momentum-based scheme can be used to accelerate the power method, but achieving an optimal convergence rate with existing algorithms critically relies on additional spectral information that is unavailable at run-time, and sub-optimal initializations can result in divergence. In this paper, we provide a pair of novel momentum-based power methods, which we call the delayed momentum power method (DMPower) and a streaming variant, the delayed momentum streaming method (DMStream). Our methods leverage inexact deflation and are capable of achieving near-optimal convergence with far less restrictive hyperparameter requirements. We provide convergence analyses for both algorithms through the lens of perturbation theory. Further, we experimentally demonstrate that DMPower routinely outperforms the vanilla power method and that both algorithms match the convergence speed of an oracle running existing accelerated methods with perfect spectral knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge