Face Alignment using a 3D Deeply-initialized Ensemble of Regression Trees

Face alignment algorithms locate a set of landmark points in images of faces taken in unrestricted situations. State-of-the-art approaches typically fail or lose accuracy in the presence of occlusions, strong deformations, large pose variations and ambiguous configurations. In this paper we present 3DDE, a robust and efficient face alignment algorithm based on a coarse-to-fine cascade of ensembles of regression trees. It is initialized by robustly fitting a 3D face model to the probability maps produced by a convolutional neural network. With this initialization we address self-occlusions and large face rotations. Further, the regressor implicitly imposes a prior face shape on the solution, addressing occlusions and ambiguous face configurations. Its coarse-to-fine structure tackles the combinatorial explosion of parts deformation. In the experiments performed, 3DDE improves the state-of-the-art in 300W, COFW, AFLW and WFLW data sets. Finally, given that 3DDE can also be trained with missing and occluded landmarks, we have been able to perform cross-dataset experiments that reveal the existence of a significant data set bias in these benchmarks.

Geometrical analysis of polynomial lens distortion models

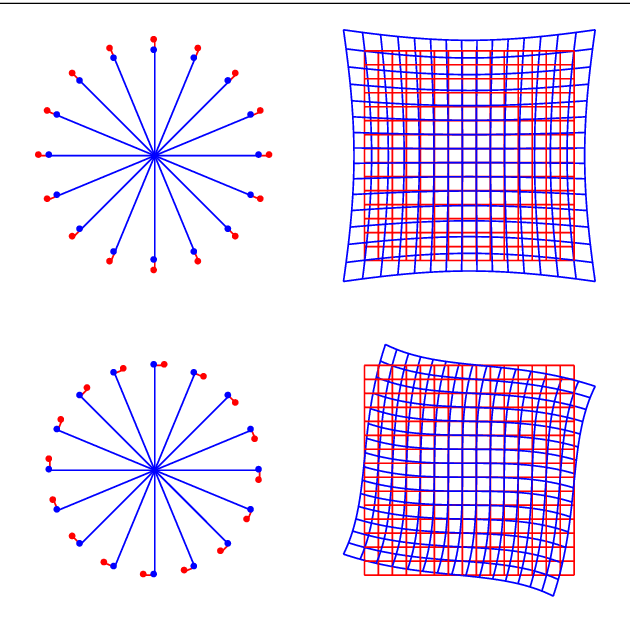
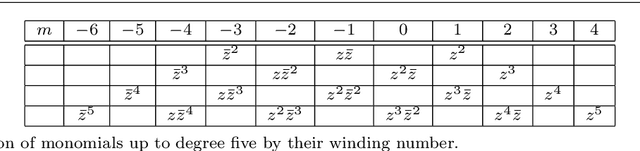
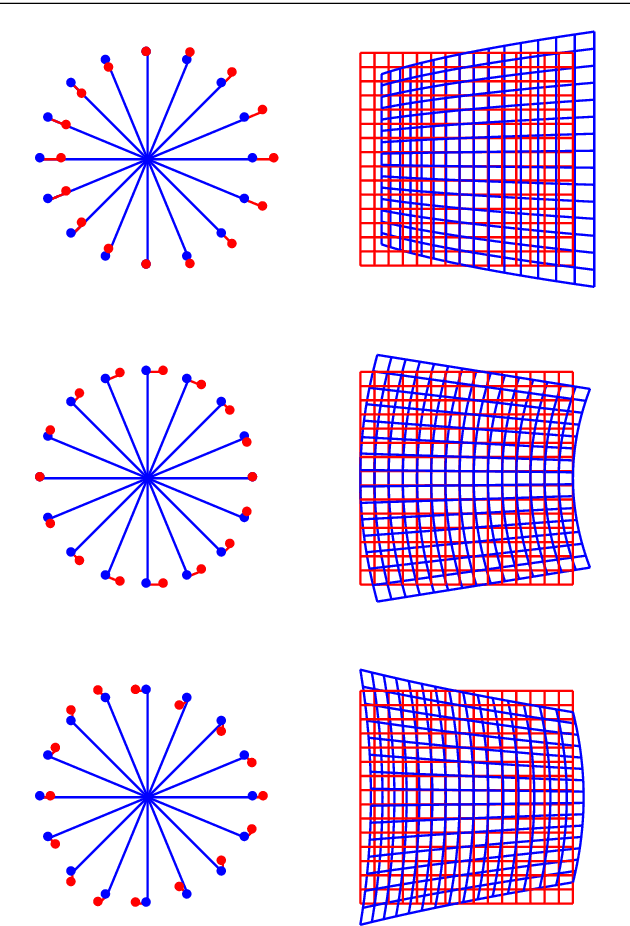
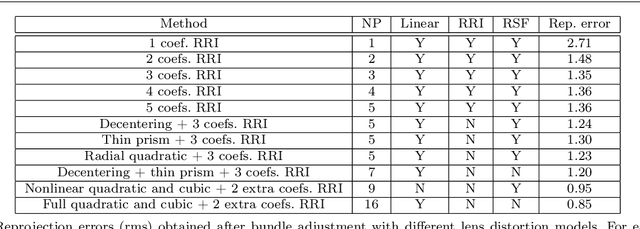
Polynomial functions are a usual choice to model the nonlinearity of lenses. Typically, these models are obtained through physical analysis of the lens system or on purely empirical grounds. The aim of this work is to facilitate an alternative approach to the selection or design of these models based on establishing a priori the desired geometrical properties of the distortion functions. With this purpose we obtain all the possible isotropic linear models and also those that are formed by functions with symmetry with respect to some axis. In this way, the classical models (decentering, thin prism distortion) are found to be particular instances of the family of models found by geometric considerations. These results allow to find generalizations of the most usually employed models while preserving the desired geometrical properties. Our results also provide a better understanding of the geometric properties of the models employed in the most usual computer vision software libraries.

Autocalibration with the Minimum Number of Cameras with Known Pixel Shape

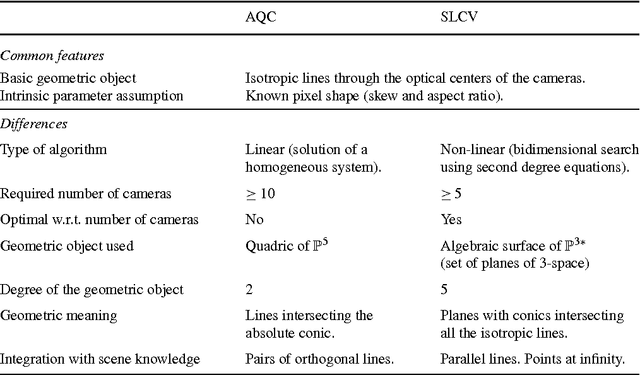
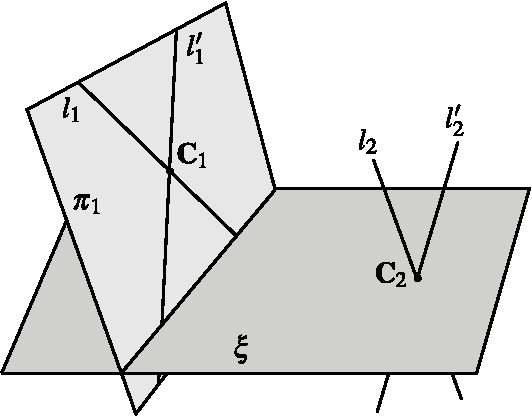
In 3D reconstruction, the recovery of the calibration parameters of the cameras is paramount since it provides metric information about the observed scene, e.g., measures of angles and ratios of distances. Autocalibration enables the estimation of the camera parameters without using a calibration device, but by enforcing simple constraints on the camera parameters. In the absence of information about the internal camera parameters such as the focal length and the principal point, the knowledge of the camera pixel shape is usually the only available constraint. Given a projective reconstruction of a rigid scene, we address the problem of the autocalibration of a minimal set of cameras with known pixel shape and otherwise arbitrarily varying intrinsic and extrinsic parameters. We propose an algorithm that only requires 5 cameras (the theoretical minimum), thus halving the number of cameras required by previous algorithms based on the same constraint. To this purpose, we introduce as our basic geometric tool the six-line conic variety (SLCV), consisting in the set of planes intersecting six given lines of 3D space in points of a conic. We show that the set of solutions of the Euclidean upgrading problem for three cameras with known pixel shape can be parameterized in a computationally efficient way. This parameterization is then used to solve autocalibration from five or more cameras, reducing the three-dimensional search space to a two-dimensional one. We provide experiments with real images showing the good performance of the technique.