Geometrical analysis of polynomial lens distortion models
Paper and Code
Jul 30, 2018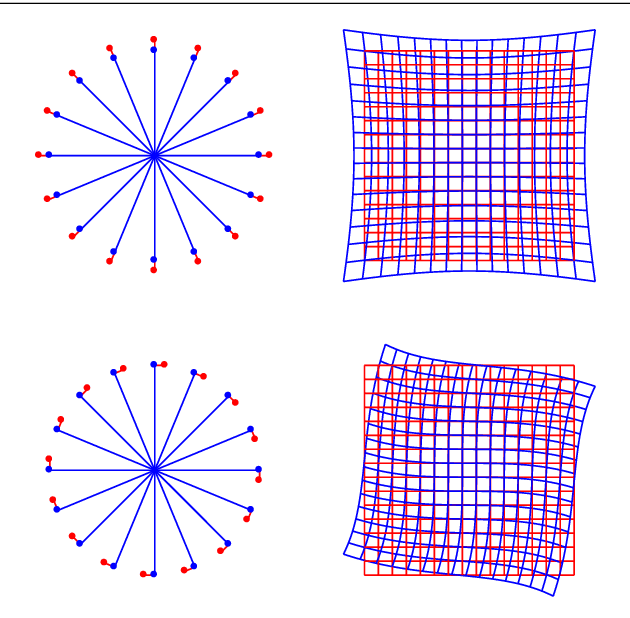
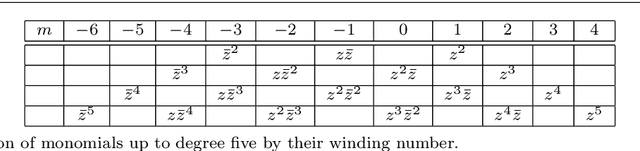
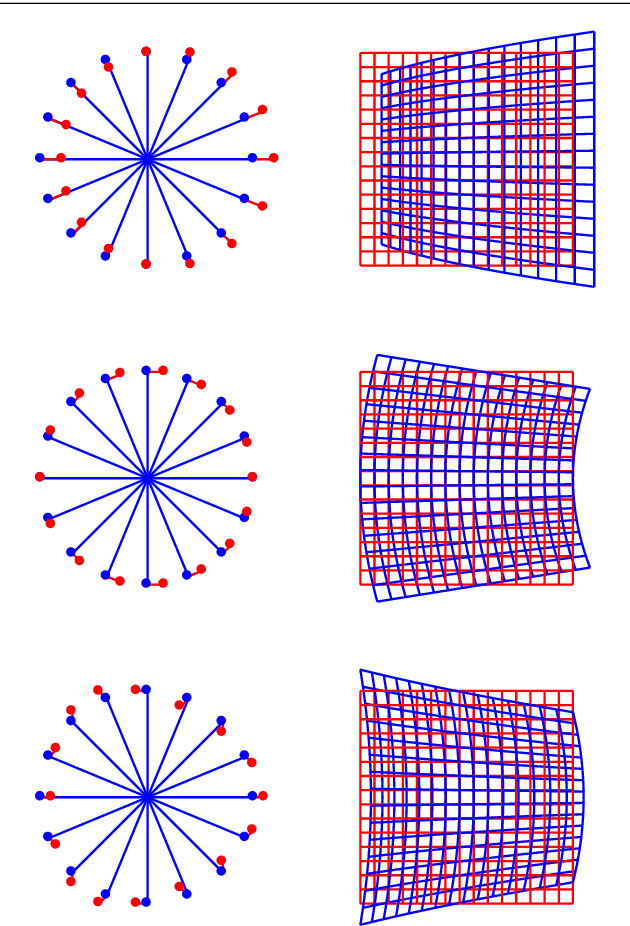
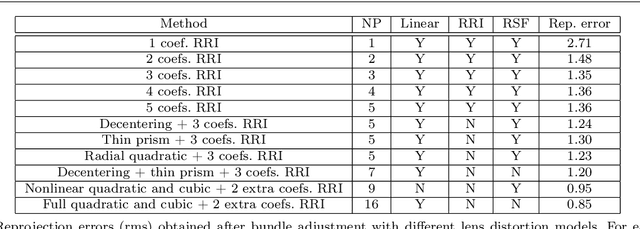
Polynomial functions are a usual choice to model the nonlinearity of lenses. Typically, these models are obtained through physical analysis of the lens system or on purely empirical grounds. The aim of this work is to facilitate an alternative approach to the selection or design of these models based on establishing a priori the desired geometrical properties of the distortion functions. With this purpose we obtain all the possible isotropic linear models and also those that are formed by functions with symmetry with respect to some axis. In this way, the classical models (decentering, thin prism distortion) are found to be particular instances of the family of models found by geometric considerations. These results allow to find generalizations of the most usually employed models while preserving the desired geometrical properties. Our results also provide a better understanding of the geometric properties of the models employed in the most usual computer vision software libraries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge