Antonio M. Sudoso
Exact and Heuristic Algorithms for Constrained Biclustering
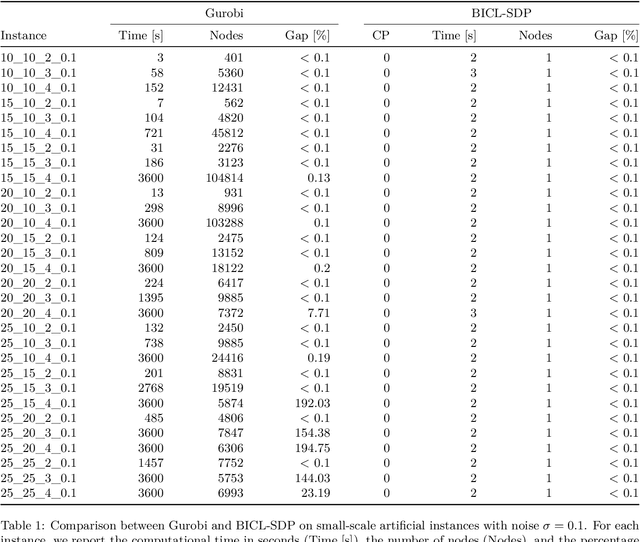
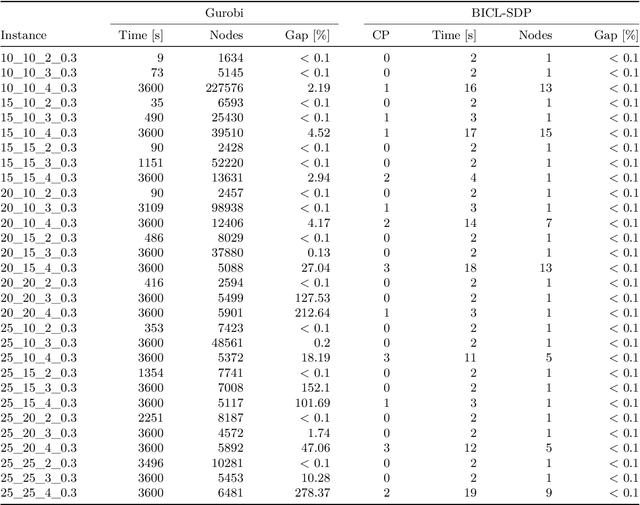
Aug 07, 2025Abstract:Biclustering, also known as co-clustering or two-way clustering, simultaneously partitions the rows and columns of a data matrix to reveal submatrices with coherent patterns. Incorporating background knowledge into clustering to enhance solution quality and interpretability has attracted growing interest in mathematical optimization and machine learning research. Extending this paradigm to biclustering enables prior information to guide the joint grouping of rows and columns. We study constrained biclustering with pairwise constraints, namely must-link and cannot-link constraints, which specify whether objects should belong to the same or different biclusters. As a model problem, we address the constrained version of the k-densest disjoint biclique problem, which aims to identify k disjoint complete bipartite subgraphs (called bicliques) in a weighted complete bipartite graph, maximizing the total density while satisfying pairwise constraints. We propose both exact and heuristic algorithms. The exact approach is a tailored branch-and-cut algorithm based on a low-dimensional semidefinite programming (SDP) relaxation, strengthened with valid inequalities and solved in a cutting-plane fashion. Exploiting integer programming tools, a rounding scheme converts SDP solutions into feasible biclusterings at each node. For large-scale instances, we introduce an efficient heuristic based on the low-rank factorization of the SDP. The resulting nonlinear optimization problem is tackled with an augmented Lagrangian method, where the subproblem is solved by decomposition through a block-coordinate projected gradient algorithm. Extensive experiments on synthetic and real-world datasets show that the exact method significantly outperforms general-purpose solvers, while the heuristic achieves high-quality solutions efficiently on large instances.
Strong bounds for large-scale Minimum Sum-of-Squares Clustering
Feb 12, 2025Abstract:Clustering is a fundamental technique in data analysis and machine learning, used to group similar data points together. Among various clustering methods, the Minimum Sum-of-Squares Clustering (MSSC) is one of the most widely used. MSSC aims to minimize the total squared Euclidean distance between data points and their corresponding cluster centroids. Due to the unsupervised nature of clustering, achieving global optimality is crucial, yet computationally challenging. The complexity of finding the global solution increases exponentially with the number of data points, making exact methods impractical for large-scale datasets. Even obtaining strong lower bounds on the optimal MSSC objective value is computationally prohibitive, making it difficult to assess the quality of heuristic solutions. We address this challenge by introducing a novel method to validate heuristic MSSC solutions through optimality gaps. Our approach employs a divide-and-conquer strategy, decomposing the problem into smaller instances that can be handled by an exact solver. The decomposition is guided by an auxiliary optimization problem, the "anticlustering problem", for which we design an efficient heuristic. Computational experiments demonstrate the effectiveness of the method for large-scale instances, achieving optimality gaps below 3% in most cases while maintaining reasonable computational times. These results highlight the practicality of our approach in assessing feasible clustering solutions for large datasets, bridging a critical gap in MSSC evaluation.
A column generation algorithm with dynamic constraint aggregation for minimum sum-of-squares clustering
Oct 08, 2024Abstract:The minimum sum-of-squares clustering problem (MSSC), also known as $k$-means clustering, refers to the problem of partitioning $n$ data points into $k$ clusters, with the objective of minimizing the total sum of squared Euclidean distances between each point and the center of its assigned cluster. We propose an efficient algorithm for solving large-scale MSSC instances, which combines column generation (CG) with dynamic constraint aggregation (DCA) to effectively reduce the number of constraints considered in the CG master problem. DCA was originally conceived to reduce degeneracy in set partitioning problems by utilizing an aggregated restricted master problem obtained from a partition of the set partitioning constraints into disjoint clusters. In this work, we explore the use of DCA within a CG algorithm for MSSC exact solution. Our method is fine-tuned by a series of ablation studies on DCA design choices, and is demonstrated to significantly outperform existing state-of-the-art exact approaches available in the literature.
An SDP-based Branch-and-Cut Algorithm for Biclustering
Mar 17, 2024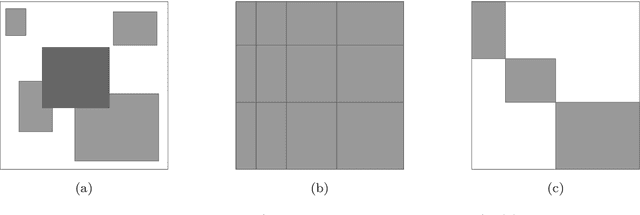
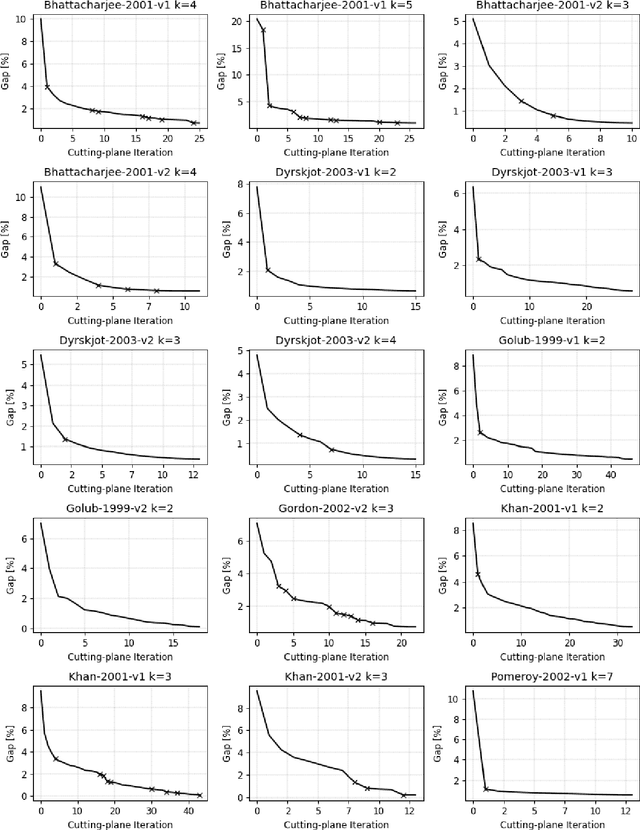
Abstract:Biclustering, also called co-clustering, block clustering, or two-way clustering, involves the simultaneous clustering of both the rows and columns of a data matrix into distinct groups, such that the rows and columns within a group display similar patterns. As a model problem for biclustering, we consider the $k$-densest-disjoint biclique problem, whose goal is to identify $k$ disjoint complete bipartite subgraphs (called bicliques) of a given weighted complete bipartite graph such that the sum of their densities is maximized. To address this problem, we present a tailored branch-and-cut algorithm. For the upper bound routine, we consider a semidefinite programming relaxation and propose valid inequalities to strengthen the bound. We solve this relaxation in a cutting-plane fashion using a first-order method. For the lower bound, we design a maximum weight matching rounding procedure that exploits the solution of the relaxation solved at each node. Computational results on both synthetic and real-world instances show that the proposed algorithm can solve instances approximately 20 times larger than those handled by general-purpose solvers.
Optimization meets Machine Learning: An Exact Algorithm for Semi-Supervised Support Vector Machines
Dec 15, 2023Abstract:Support vector machines (SVMs) are well-studied supervised learning models for binary classification. In many applications, large amounts of samples can be cheaply and easily obtained. What is often a costly and error-prone process is to manually label these instances. Semi-supervised support vector machines (S3VMs) extend the well-known SVM classifiers to the semi-supervised approach, aiming at maximizing the margin between samples in the presence of unlabeled data. By leveraging both labeled and unlabeled data, S3VMs attempt to achieve better accuracy and robustness compared to traditional SVMs. Unfortunately, the resulting optimization problem is non-convex and hence difficult to solve exactly. In this paper, we present a new branch-and-cut approach for S3VMs using semidefinite programming (SDP) relaxations. We apply optimality-based bound tightening to bound the feasible set. Box constraints allow us to include valid inequalities, strengthening the lower bound. The resulting SDP relaxation provides bounds significantly stronger than the ones available in the literature. For the upper bound, instead, we define a local search exploiting the solution of the SDP relaxation. Computational results highlight the efficiency of the algorithm, showing its capability to solve instances with a number of data points 10 times larger than the ones solved in the literature.
Multi-task learning of convex combinations of forecasting models
Oct 31, 2023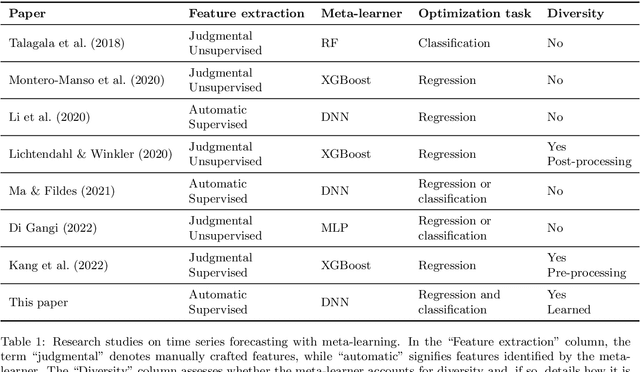
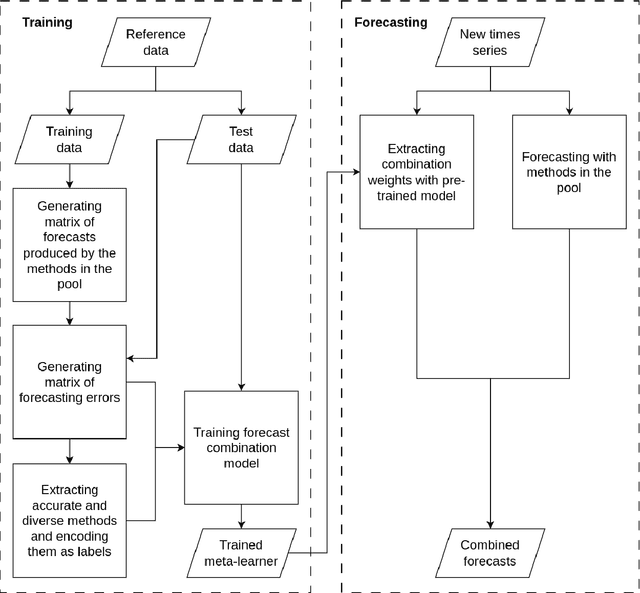

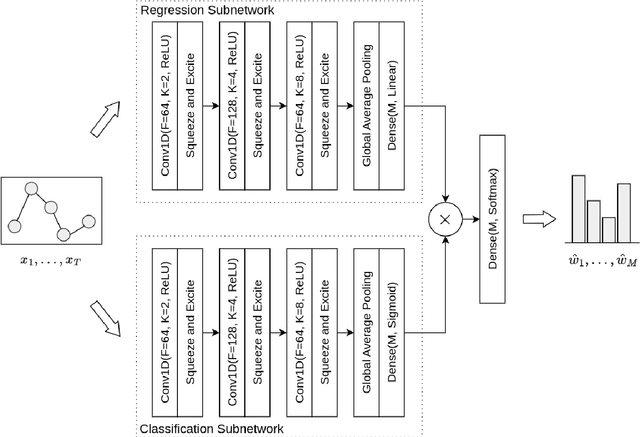
Abstract:Forecast combination involves using multiple forecasts to create a single, more accurate prediction. Recently, feature-based forecasting has been employed to either select the most appropriate forecasting models or to learn the weights of their convex combination. In this paper, we present a multi-task learning methodology that simultaneously addresses both problems. This approach is implemented through a deep neural network with two branches: the regression branch, which learns the weights of various forecasting methods by minimizing the error of combined forecasts, and the classification branch, which selects forecasting methods with an emphasis on their diversity. To generate training labels for the classification task, we introduce an optimization-driven approach that identifies the most appropriate methods for a given time series. The proposed approach elicits the essential role of diversity in feature-based forecasting and highlights the interplay between model combination and model selection when learning forecasting ensembles. Experimental results on a large set of series from the M4 competition dataset show that our proposal enhances point forecast accuracy compared to state-of-the-art methods.
Predicting municipalities in financial distress: a machine learning approach enhanced by domain expertise
Feb 11, 2023Abstract:Financial distress of municipalities, although comparable to bankruptcy of private companies, has a far more serious impact on the well-being of communities. For this reason, it is essential to detect deficits as soon as possible. Predicting financial distress in municipalities can be a complex task, as it involves understanding a wide range of factors that can affect a municipality's financial health. In this paper, we evaluate machine learning models to predict financial distress in Italian municipalities. Accounting judiciary experts have specialized knowledge and experience in evaluating the financial performance of municipalities, and they use a range of financial and general indicators to make their assessments. By incorporating these indicators in the feature extraction process, we can ensure that the predictive model is taking into account a wide range of information that is relevant to the financial health of municipalities. The results of this study indicate that using machine learning models in combination with the knowledge of accounting judiciary experts can aid in the early detection of financial distress in municipalities, leading to better outcomes for the communities they serve.
Global Optimization for Cardinality-constrained Minimum Sum-of-Squares Clustering via Semidefinite Programming
Sep 25, 2022



Abstract:The minimum sum-of-squares clustering (MSSC), or k-means type clustering, has been recently extended to exploit prior knowledge on the cardinality of each cluster. Such knowledge is used to increase performance as well as solution quality. In this paper, we propose an exact approach based on the branch-and-cut technique to solve the cardinality-constrained MSSC. For the lower bound routine, we use the semidefinite programming (SDP) relaxation recently proposed by Rujeerapaiboon et al. [SIAM J. Optim. 29(2), 1211-1239, (2019)]. However, this relaxation can be used in a branch-and-cut method only for small-size instances. Therefore, we derive a new SDP relaxation that scales better with the instance size and the number of clusters. In both cases, we strengthen the bound by adding polyhedral cuts. Benefiting from a tailored branching strategy which enforces pairwise constraints, we reduce the complexity of the problems arising in the children nodes. For the upper bound, instead, we present a local search procedure that exploits the solution of the SDP relaxation solved at each node. Computational results show that the proposed algorithm globally solves, for the first time, real-world instances of size 10 times larger than those solved by state-of-the-art exact methods.
An Exact Algorithm for Semi-supervised Minimum Sum-of-Squares Clustering
Nov 30, 2021



Abstract:The minimum sum-of-squares clustering (MSSC), or k-means type clustering, is traditionally considered an unsupervised learning task. In recent years, the use of background knowledge to improve the cluster quality and promote interpretability of the clustering process has become a hot research topic at the intersection of mathematical optimization and machine learning research. The problem of taking advantage of background information in data clustering is called semi-supervised or constrained clustering. In this paper, we present a new branch-and-bound algorithm for semi-supervised MSSC, where background knowledge is incorporated as pairwise must-link and cannot-link constraints. For the lower bound procedure, we solve the semidefinite programming relaxation of the MSSC discrete optimization model, and we use a cutting-plane procedure for strengthening the bound. For the upper bound, instead, by using integer programming tools, we propose an adaptation of the k-means algorithm to the constrained case. For the first time, the proposed global optimization algorithm efficiently manages to solve real-world instances up to 800 data points with different combinations of must-link and cannot-link constraints and with a generic number of features. This problem size is about four times larger than the one of the instances solved by state-of-the-art exact algorithms.
A machine learning approach for forecasting hierarchical time series
May 31, 2020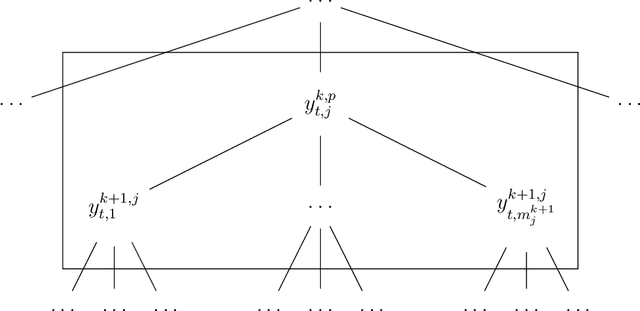



Abstract:In this paper, we propose a machine learning approach for forecasting hierarchical time series. Rather than using historical or forecasted proportions, as in standard top-down approaches, we formulate the disaggregation problem as a non-linear regression problem. We propose a deep neural network that automatically learns how to distribute the top-level forecasts to the bottom level-series of the hierarchy, keeping into account the characteristics of the aggregate series and the information of the individual series. In order to evaluate the performance of the proposed method, we analyze hierarchical sales data and electricity demand data. Besides comparison with the top-down approaches, the model is compared with the bottom-up method and the optimal reconciliation method. Results demonstrate that our method does not only increase the average forecasting accuracy of the hierarchy but also addresses the need of building an automated procedure generating coherent forecasts for many time series at the same time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge