An SDP-based Branch-and-Cut Algorithm for Biclustering
Paper and Code
Mar 17, 2024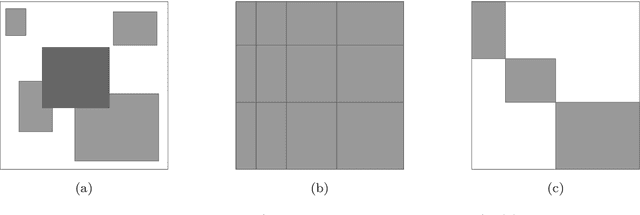
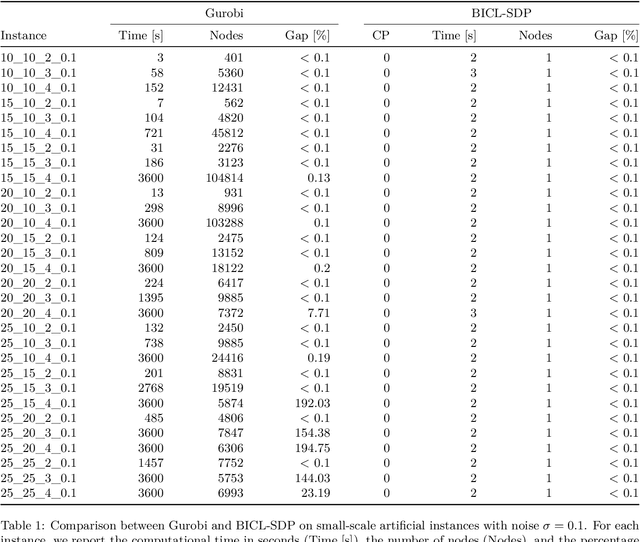
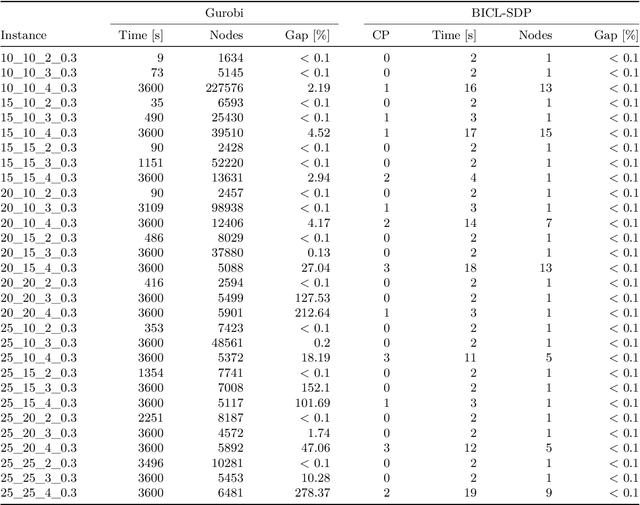
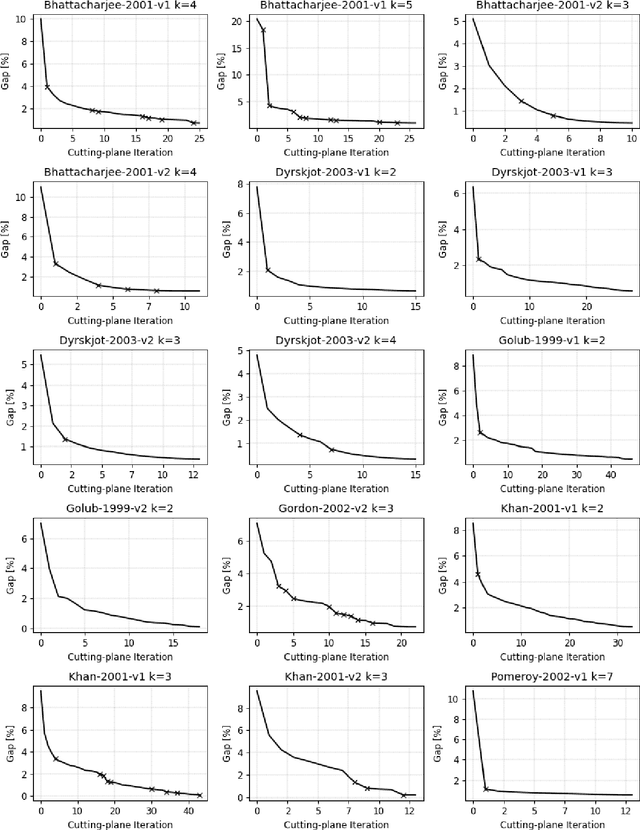
Biclustering, also called co-clustering, block clustering, or two-way clustering, involves the simultaneous clustering of both the rows and columns of a data matrix into distinct groups, such that the rows and columns within a group display similar patterns. As a model problem for biclustering, we consider the $k$-densest-disjoint biclique problem, whose goal is to identify $k$ disjoint complete bipartite subgraphs (called bicliques) of a given weighted complete bipartite graph such that the sum of their densities is maximized. To address this problem, we present a tailored branch-and-cut algorithm. For the upper bound routine, we consider a semidefinite programming relaxation and propose valid inequalities to strengthen the bound. We solve this relaxation in a cutting-plane fashion using a first-order method. For the lower bound, we design a maximum weight matching rounding procedure that exploits the solution of the relaxation solved at each node. Computational results on both synthetic and real-world instances show that the proposed algorithm can solve instances approximately 20 times larger than those handled by general-purpose solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge