DBGSL: Dynamic Brain Graph Structure Learning

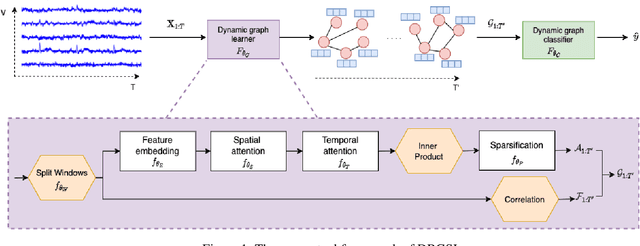
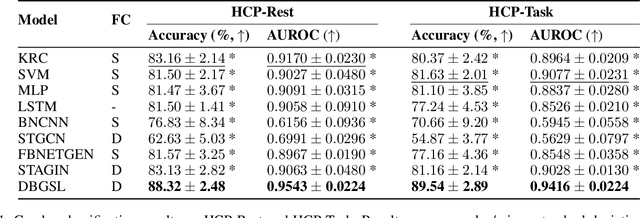
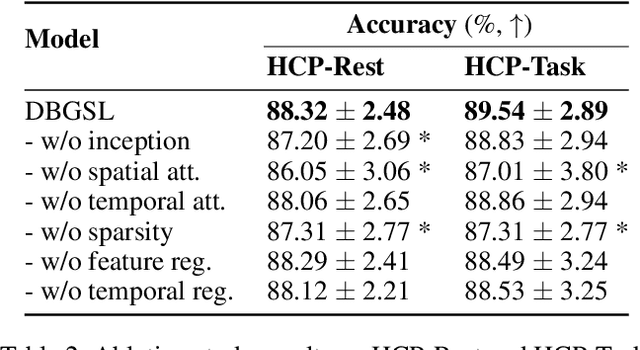
Functional connectivity (FC) between regions of the brain is commonly estimated through statistical dependency measures applied to functional magnetic resonance imaging (fMRI) data. The resulting functional connectivity matrix (FCM) is often taken to represent the adjacency matrix of a brain graph. Recently, graph neural networks (GNNs) have been successfully applied to FCMs to learn brain graph representations. A common limitation of existing GNN approaches, however, is that they require the graph adjacency matrix to be known prior to model training. As such, it is implicitly assumed the ground-truth dependency structure of the data is known. Unfortunately, for fMRI this is not the case as the choice of which statistical measure best represents the dependency structure of the data is non-trivial. Also, most GNN applications to fMRI assume FC is static over time, which is at odds with neuroscientific evidence that functional brain networks are time-varying and dynamic. These compounded issues can have a detrimental effect on the capacity of GNNs to learn representations of brain graphs. As a solution, we propose Dynamic Brain Graph Structure Learning (DBGSL), a supervised method for learning the optimal time-varying dependency structure of fMRI data. Specifically, DBGSL learns a dynamic graph from fMRI timeseries via spatial-temporal attention applied to brain region embeddings. The resulting graph is then fed to a spatial-temporal GNN to learn a graph representation for classification. Experiments on large resting-state as well as task fMRI datasets for the task of gender classification demonstrate that DBGSL achieves state-of-the-art performance. Moreover, analysis of the learnt dynamic graphs highlights prediction-related brain regions which align with findings from existing neuroscience literature.

Text Classification with Compression Algorithms

This work concerns a comparison of SVM kernel methods in text categorization tasks. In particular I define a kernel function that estimates the similarity between two objects computing by their compressed lengths. In fact, compression algorithms can detect arbitrarily long dependencies within the text strings. Data text vectorization looses information in feature extractions and is highly sensitive by textual language. Furthermore, these methods are language independent and require no text preprocessing. Moreover, the accuracy computed on the datasets (Web-KB, 20ng and Reuters-21578), in some case, is greater than Gaussian, linear and polynomial kernels. The method limits are represented by computational time complexity of the Gram matrix and by very poor performance on non-textual datasets.