Likelihood Based Inference in Fully and Partially Observed Exponential Family Graphical Models with Intractable Normalizing Constants

Probabilistic graphical models that encode an underlying Markov random field are fundamental building blocks of generative modeling to learn latent representations in modern multivariate data sets with complex dependency structures. Among these, the exponential family graphical models are especially popular, given their fairly well-understood statistical properties and computational scalability to high-dimensional data based on pseudo-likelihood methods. These models have been successfully applied in many fields, such as the Ising model in statistical physics and count graphical models in genomics. Another strand of models allows some nodes to be latent, so as to allow the marginal distribution of the observable nodes to depart from exponential family to capture more complex dependence. These approaches form the basis of generative models in artificial intelligence, such as the Boltzmann machines and their restricted versions. A fundamental barrier to likelihood-based (i.e., both maximum likelihood and fully Bayesian) inference in both fully and partially observed cases is the intractability of the likelihood. The usual workaround is via adopting pseudo-likelihood based approaches, following the pioneering work of Besag (1974). The goal of this paper is to demonstrate that full likelihood based analysis of these models is feasible in a computationally efficient manner. The chief innovation lies in using a technique of Geyer (1991) to estimate the intractable normalizing constant, as well as its gradient, for intractable graphical models. Extensive numerical results, supporting theory and comparisons with pseudo-likelihood based approaches demonstrate the applicability of the proposed method.

Nearest Neighbor Dirichlet Process

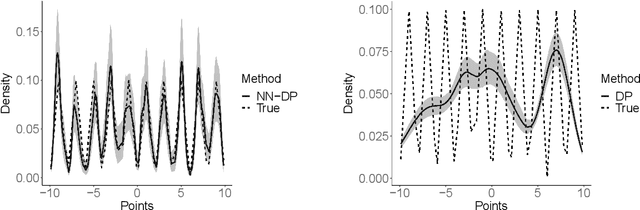
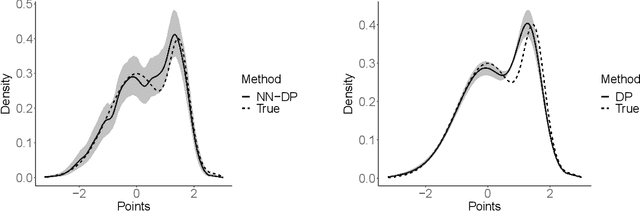
There is a rich literature on Bayesian nonparametric methods for unknown densities. The most popular approach relies on Dirichlet process mixture models. These models characterize the unknown density as a kernel convolution with an unknown almost surely discrete mixing measure, which is given a Dirichlet process prior. Such models are very flexible and have good performance in many settings, but posterior computation relies on Markov chain Monte Carlo algorithms that can be complex and inefficient. As a simple and general alternative, we propose a class of nearest neighbor-Dirichlet processes. The approach starts by grouping the data into neighborhoods based on standard algorithms. Within each neighborhood, the density is characterized via a Bayesian parametric model, such as a Gaussian with unknown parameters. Assigning a Dirichlet prior to the weights on these local kernels, we obtain a simple pseudo-posterior for the weights and kernel parameters. A simple and embarrassingly parallel Monte Carlo algorithm is proposed to sample from the resulting pseudo-posterior for the unknown density. Desirable asymptotic properties are shown, and the methods are evaluated in simulation studies and applied to a motivating dataset in the context of classification.